This script provides an example of autocorrelated residuals.

Dataset description

US Macroeconomics Data Set, Quarterly, 1950I to 2000IV, 204 Quarterly Observations
Source: Department of Commerce, BEA website and www.economagic.com

Feild Name Definition
year Year
qtr Quarter
realgdp Real GDP ($bil)
realcons Real consumption expenditures
realinvs Real investment by private sector
realgovt Real government expenditures
realdpi Real disposable personal income
cpi_u Consumer price index
M1 Nominal money stock
tbilrate Quarterly average of month end 90 day t bill rate
unemp Unemployment rate
pop Population, mil. interpolate of year end figures using constant growth rate per quarter
infl Rate of inflation (First observation is missing)
realint Ex post real interest rate = Tbilrate - Infl. (First observation is missing) 
# data preview
data <- read.table("https://raw.githubusercontent.com/my1396/course_dataset/refs/heads/main/TableF5-2.txt", header = TRUE)
data <- data %>% 
    mutate(delta_infl = infl-lag(infl))
data %>% 
    head() %>% 
    knitr::kable(digits = 5) %>%
    kable_styling(bootstrap_options = c("striped", "hover"), full_width = FALSE, latex_options="scale_down") %>% 
    scroll_box(width = "100%")
Year qtr realgdp realcons realinvs realgovt realdpi cpi_u M1 tbilrate unemp pop infl realint delta_infl
1950 1 1610.5 1058.9 198.1 361.0 1186.1 70.6 110.20 1.12 6.4 149.461 0.0000 0.0000
1950 2 1658.8 1075.9 220.4 366.4 1178.1 71.4 111.75 1.17 5.6 150.260 4.5071 -3.3404 4.5071
1950 3 1723.0 1131.0 239.7 359.6 1196.5 73.2 112.95 1.23 4.6 151.064 9.9590 -8.7290 5.4519
1950 4 1753.9 1097.6 271.8 382.5 1210.0 74.9 113.93 1.35 4.2 151.871 9.1834 -7.8301 -0.7756
1951 1 1773.5 1122.8 242.9 421.9 1207.9 77.3 115.08 1.40 3.5 152.393 12.6160 -11.2160 3.4326
1951 2 1803.7 1091.4 249.2 480.1 1225.8 77.6 116.19 1.53 3.1 152.917 1.5494 -0.0161 -11.0666

Empirical model

\[ \Delta I_t = \beta_1 + \beta_2 u_t + \varepsilon_t \] where

  • \(I_t\) is the inflation rate; \(\Delta I_t = I_t - I_{t-1}\) is the first difference of the inflation rate;
  • \(u_t\) is the unemployment rate;
  • \(\varepsilon_t\) is the error term.

We remove the first two quarters due to missing value in the first observation and the change in the rate of inflation.

Regression result for OLS.

lm_phillips <- lm(delta_infl ~ unemp, data = data %>% tail(-2))
stargazer(lm_phillips, 
          type = "html", 
          title = "Phillips Curve Regression",
          notes = "<span>&#42;</span>: p<0.1; <span>&#42;&#42;</span>: <strong>p<0.05</strong>; <span>&#42;&#42;&#42;</span>: p<0.01 <br> Standard errors in parentheses.",
          notes.append = F)
Phillips Curve Regression
Dependent variable:
delta_infl
unemp -0.090
(0.126)
Constant 0.492
(0.740)
Observations 202
R2 0.003
Adjusted R2 -0.002
Residual Std. Error 2.822 (df = 200)
F Statistic 0.513 (df = 1; 200)
Note: *: p<0.1; **: p<0.05; ***: p<0.01
Standard errors in parentheses. 
# variance-covariance matrix
vcov(lm_phillips)
##             (Intercept)       unemp
## (Intercept)  0.54830829 -0.08973175
## unemp       -0.08973175  0.01582211

Autocorrelated residuals

Plot the residuals.

plot(lm_phillips$residuals, type="l")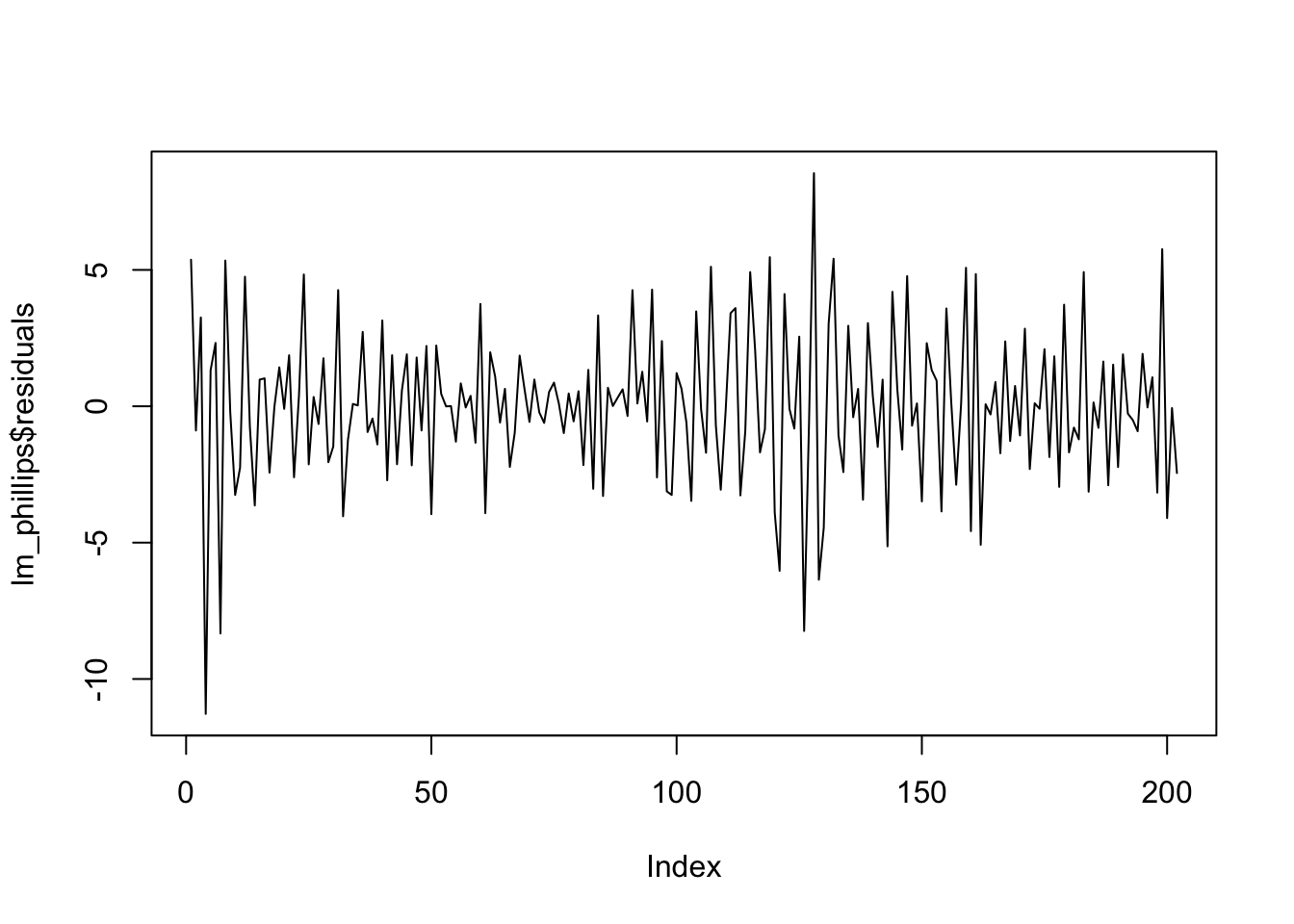
Phillips Curve Deviations from Expected Inflation

Fig. 1: Phillips Curve Deviations from Expected Inflation

Fig. 1 shows striking negative autocorrelation.

Now we test the serial correlation of the residuals. \[ \varepsilon_t = \phi\varepsilon_{t-1} + e_t \]

res <- tibble(
            res_t = lm_phillips$residuals,
            res_t1 = lag(lm_phillips$residuals))
lm_res <- lm(res_t ~ res_t1, data = res)
summary(lm_res)
## 
## Call:
## lm(formula = res_t ~ res_t1, data = res)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9.8694 -1.4800  0.0718  1.4990  8.3258 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.02155    0.17854  -0.121    0.904    
## res_t1      -0.42630    0.06355  -6.708    2e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.531 on 199 degrees of freedom
##   (1 observation deleted due to missingness)
## Multiple R-squared:  0.1844, Adjusted R-squared:  0.1803 
## F-statistic: 44.99 on 1 and 199 DF,  p-value: 2.002e-10

The regression of the least squares residuals on their past values gives a slope of -0.4263 with a highly significant \(t\) ratio of -6.7078. We thus conclude that the residuals in this models are highly negatively autocorrelated.

References:

  • Ex. 12.3, Chap 12 Serial Correlation, Econometric Analysis, Greene 5th Edition, pp 251.