↑

Trig identities

$\mathrm{sin}\theta$ 奇函数

$\mathrm{cos}\theta$ 偶函数

$\sec^2=1+\tan^2$

$\mathrm{sin}(\theta\pm\frac{k\pi}{2})$, $\mathrm{cos}(\theta\pm\frac{k\pi}{2})$ 奇变偶不变，符号看象限。

  • 根据$k$ ，决定是否变函数。 $k$ 为奇数，$\mathrm{sin}$ 变 $\mathrm{cos}$，$\mathrm{cos}$ 变 $\mathrm{sin}$。$k$ 为偶数，则函数名不变。
  • 符号由原函数决定, assuming $0<\theta<\frac{\pi}{2}$为锐角，看$\theta\pm\frac{k\pi}{2}$在原函数的正负。实际上 $\theta$ 可以是任意角度，但如果是钝角，完全可以$k:=k+1$化为锐角；否则，函数处于未化简完全的状态。
  • e.g., $\mathrm{cos}(\frac{\pi}{2}-\theta)=\mathrm{sin}\theta$, $k=1$为奇数, 函数名变为$\mathrm{sin}$; 当$\theta$为锐角时，$\frac{\pi}{2}-\theta$ 在第一象限，$\mathrm{cos}(\frac{\pi}{2}-\theta)$为正。

double-angel formula 倍角公式

  • $\mathrm{cos}(2\theta)=\mathrm{cos}^2\theta-\mathrm{sin}^2\theta$

  • $\mathrm{sin}(2\theta)=2\mathrm{sin}\theta\cdot \mathrm{cos}\theta$, 2 不要落下了！

half-angel formula 半角公式 (降幂公式) used to get rid of the power

  • $\mathrm{cos}^2\theta=\frac{1+\mathrm{cos}(2\theta)}{2}$

  • $\mathrm{sin}^2\theta=\frac{1-\mathrm{cos}(2\theta)}{2}$

和差公式 Angle sum and difference identities

$\mathrm{sin}(\alpha+\beta)=\mathrm{sin}\alpha\cdot\mathrm{cos}\beta+\mathrm{cos}\alpha\cdot\mathrm{sin}\beta$

$\mathrm{sin}(\alpha-\beta)=\mathrm{sin}\alpha\cdot\mathrm{cos}\beta-\mathrm{cos}\alpha\cdot\mathrm{sin}\beta$

$\mathrm{cos}(\alpha+\beta)=\mathrm{cos}\alpha\cdot\mathrm{cos}\beta-\mathrm{sin}\alpha\cdot\mathrm{sin}\beta$

$\mathrm{cos}(\alpha-\beta)=\mathrm{cos}\alpha\cdot\mathrm{cos}\beta+\mathrm{sin}\alpha\cdot\mathrm{sin}\beta$

积化和差公式可以由和差公式得来。(product-to-sum identities)

和差化积公式 (sum-to-product identities)

正加正，正在前； $\mathrm{sin}\alpha +\mathrm{sin}\beta=2\, \mathrm{sin}\frac{\alpha+\beta}{2}\cdot\mathrm{cos}\frac{\alpha-\beta}{2}$

正减余在先； $\mathrm{sin}\alpha - \mathrm{sin}\beta=2\, \mathrm{cos}\frac{\alpha+\beta}{2}\cdot\mathrm{sin}\frac{\alpha-\beta}{2}$

余加全是余；$\mathrm{cos}\alpha +\mathrm{cos}\beta=2\, \mathrm{cos}\frac{\alpha+\beta}{2}\cdot\mathrm{cos}\frac{\alpha-\beta}{2}$

余减负正弦；$\mathrm{cos}\alpha - \mathrm{cos}\beta=-2\, \mathrm{sin}\frac{\alpha+\beta}{2}\cdot\mathrm{sin}\frac{\alpha-\beta}{2}$

Calculus

1st derivative

$y’(x)=0$ max/min point, change of directions (from up to down if max, from down to up if min).

2nd derivative

$y^{\prime\prime}=0$ inflection point, change of concavity.

Notation

The partial derivative is denoted by the symbol $\partial$, which replaces the roman letter $\mathrm{d}$ used to denote a full/ total derivative.

Given a function $f(x,y)$, the first and second partial derivatives of $f$ with respect to $x$ can be denoted by:

\[\dfrac{\partial f}{\partial x} \text{ and } \dfrac{\partial^2f}{\partial x^2}.\]

Partial derivatives can also be denoted by a subscript, where the subscript specifies which variable to differentiate with respect to. The first and second partial derivatives of $f$ with respect to $x$ can also be denoted by:

\[f_x \text{ and } f_{xx}\]

The first and second partial derivatives of $f$ with respect to $y$ can be denoted by:

\[\dfrac{\partial f}{\partial y} \text{ and } \dfrac{\partial^2f}{\partial y^2}.\]

or using the subscript

\[f_y \text{ and } f_{yy}.\]

Mixed derivative of $f$ can be denoted in the following ways:

\[\dfrac{\partial}{\partial x}\left(\dfrac{\partial f}{\partial y}\right)=\dfrac{\partial^2f}{\partial x \partial y}=f_{yx},\] \[\dfrac{\partial}{\partial y}\left(\dfrac{\partial f}{\partial x}\right)=\dfrac{\partial^2f}{\partial y\partial x}=f_{xy}.\]
  • $\dfrac{\partial^2f}{\partial y\partial x}=f_{xy}$ denotes that the derivative is first taken with respect to $x$, and then with respect to $y$,
  • $\dfrac{\partial^2f}{\partial x\partial y}=f_{yx}$ denotes that the derivative is first taken with respect to $y$, and then with respect to $x$.
  • Mixed partial derivatives $f_{xy}$ and $f_{yx}$ are always equal, called “symmetry of mixed derivatives”.
  • Differentiate from the marginal density function. The marginal probability density function of $X$ can be obtained by integrating the joint probability distribution, $f(x,y)$, over $Y$, and vice versa. $f_{X}(x)=\int f(x,y)\,dy$ and $f_{Y}(x)=\int f(x,y)\,dx$

Brackets with subscripts are commonly used to indicate which variables are held constant.

Given a function $f(x,y,z)$, the partial derivative of $f$ with respect to $x$, where $y,z$ are held constant, can be denoted by:

\[\left(\dfrac{\partial f}{\partial x}\right)_{y,z}.\]

Another variant is using a vertical bar

\[\left . \dfrac{\partial f}{\partial x} \right \vert _{y,z}.\]

Convex function $\cup$

  • The line segment between any two distinct points lies above the graph between the two points.
  • 2nd derivative $f’’$ is nonnegative, i.e., $f’$ is monotonically increasing.

Concave function $\cap$

  • The line segment between any two distinct points lies below the graph between the two points.
  • 2nd derivative $f’’$ is nonpositive, i.e., $f’$ is monotonically decreasing.

How to find min/max pt.

  • look at critical points (where $f’=0$), end points, and discontinuities. Critical values are the values of the function where $x$ equal to critical points.

    • 1st derivative rule, then you get critical points. Have to check whether it is min or max. Two ways of doing it:

      1. calculate end points and compare to critical points;

      2. calculate $f^{\prime\prime}$, if $f^{\prime\prime}<0$ then max; if $f^{\prime\prime}>0$ then min; (2nd derivate tell how 1st derivative changes. If at min, the func will increase, i.e., $f’$ $\uparrow$; if at max, the func will decrease, i.e., $f’ \downarrow$. )

      • Note: it is NOT recomended to calculate the 2nd derivative b/c usually it is easier to calculate the end points. 2nd derivatives are usually difficult to find if you have a complicated func.

  • max/min point corresponds to critical points; alternatively, where is max/min achieved?

  • max/min value corresponds to critical value;

Newton’s Method \(\begin{align*} x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} \end{align*}\) Newton’s method works well if $i$) $\vert f’\vert$ is not too small; $ii$) $\vert f^{\prime\prime}\vert$ is not too big; and $iii$) $x_0$ is nearby $x$.

Newton’s method fails: $i$) find an unexpected root (depending on where the initial guess is); $ii$) completely fail. It repeats in a cycle, and never converges to a single value.

Fail of Newton method illustration

MVT vs. IVT

MVT says let $f:[a,b]\rightarrow \mathbb{R}$ be a continuous function on the closed interval $[a,b]$, and differentiable on the open interval $(a,b)$. Then there exists some $c$ in $(a,b)$ such that \(\begin{align*} f'(c)=\frac{f(b)-f(a)}{b-a} \end{align*}\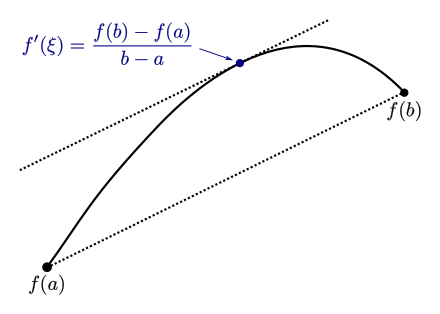) MVT.png

IVT says let $f:[a,b]\rightarrow \mathbb{R}$ be a continuous function on the closed interval $[a,b]$, $\textrm{w}$ is a number between $f(a)$ and $f(b)$, then there must be at least one value $c\in [a,b]$ such that $f(c)=\textrm{w}$.

IVT.svg

  • The mean value theorem is all about the differentiable functions and derivatives, whereas the intermediate value theorem is about the continuous function.
  • The MVT guarantees that the derivatives have certain values, whereas the IVT guarantees that the function has certain values between two given values.

Anti-differentiation used interchangeablely with Integration.

Anti-derivatives $\Longleftrightarrow$ Indefinite Integrals

Integral formulas

Trigonometric integrals

  1. $\int \frac{1}{\sqrt{1-x^2}} dx=\mathrm{sin}^{-1}x+c$, note that $\mathrm{sin}^{-1}x$ denotes “inverse sin” or $\mathrm{arcsin}(x)$, not $\frac{1}{\mathrm{sin}x}$.
  2. $\int -\frac{1}{\sqrt{1-x^2}} dx=\mathrm{cos}^{-1}x+c$
  3. $\int \frac{1}{1+x^2} dx=\mathrm{tan}^{-1}x+c$
  4. $(\tan x)’=\sec^2x$, or $\int \mathrm{sec}^2x\,dx=\mathrm{tan}x+c$.
  5. $\sec(x)’=\sec x\tan x$, or $\int \sec x\tan x\, dx=\sec x +c$.
  6. $\int \mathrm{tan}x\,dx=-\ln(\cos x)+c$.
  7. $\int \sec x\,dx=\ln(\sec x+\tan x)+c$, substitution $u=\sec x+\tan x$.

Common integrals/ derivatives

$\int\frac{1}{y}dy=\ln\vert y\vert +c$

$\sqrt{x}=\frac{1}{2\sqrt{x}}$

Inverse function

Let $y=f(x)$, then $f^{-1}(y)=x$, define $g(y)=f^{-1}(y)$.

Rewrite $x=g(y)$. Take derivative w.r.t $x$ on both sides,

\[\begin{align*} \frac{d}{dx} x &= \frac{d}{dx} g(y) \\ 1 &= \frac{dg(y)}{dy} \cdot \frac{dy}{dx} \quad \text{(by chain rule)} \\ 1 &= g'(y)\cdot f'(x) \\ g'(y) &= \frac{1}{f'(x)} \end{align*}\]

That is $[f^{-1}]’(y) = \frac{1}{f’(x)}$. Derivative of $f^{-1}$ equals to the reciprocal of the derivative of $f$, evaluated at the value of the inverse function ($x=f^{-1}(y)$).

FTC1

Let $f$ be continuous on $[a,b]$ and let $F$ be any antiderivative of $f$. Then \(\begin{align*} \int_a^bf(t)dt=F(b)-F(a) \end{align*}\)

FTC2

Let $f$ be continuous on $[a,b]$ and let $F(x)=\int_a^xf(t)dt$. Then $F$ is a differentiable function on $(a,b)$, and \(\begin{align*} F'(x)=\frac{d}{dx}\int_a^x f(t)dt=f(x). \end{align*}\)

  • Important to differentiate variable of integrand $t$ from the upper limit $x$. Use different letters!
  • The derivative of an integration is just replacing the integrand variable with the upper limit variable.

Trig integrals and Substitution

To integrate $\int \cos^jx \sin^kx\,dx$ use the following strategies:

  1. If $𝑘$ is odd, rewrite $\sin^k𝑥=\sin^{𝑘−1}𝑥\sin 𝑥$ and use the identity $\sin^2𝑥=1−\cos^2𝑥$ to rewrite $\sin^{𝑘−1}𝑥$ in terms of $\cos 𝑥$ . Integrate using the substitution $𝑢=\cos 𝑥$ . This substitution makes $𝑑𝑢=−\sin 𝑥𝑑𝑥$.

  2. If $𝑗$ is odd, rewrite $\cos^𝑗𝑥=\cos^{𝑗−1}𝑥\cos 𝑥$ and use the identity $\cos^2𝑥=1−\sin^2𝑥$ to rewrite $\mathrm{cos}^{𝑗−1}x$ in terms of $\sin 𝑥$. Integrate using the substitution $𝑢=\sin 𝑥$. This substitution makes $𝑑𝑢=\cos 𝑥𝑑𝑥$. (Note: If both $𝑗$ and $𝑘$ are odd, either strategy 1 or strategy 2 may be used.)

  3. If both $𝑗$ and $𝑘$ are even, use $\sin^2𝑥=\frac{1−\cos(2𝑥)}{2}$ and $\cos^2$𝑥=$\frac{1+\cos(2𝑥)}{2}$ . After applying these formulas, simplify and reapply strategies 1 through 3 as appropriate.

Summary:

  1. integrand only includes powers of $\mathrm{sin}x$ and $\mathrm{cos}x$.
  2. find the odd power and separate 1 as derivative of the substitution. Rewrite the integrand as a function of the other trig.
  3. if only even exponents are present, use half-angel fornula to lower the power (double the trig angel) until you have an odd exponent.

Integrating $\int \text{tan}^𝑘 𝑥\sec^𝑗 𝑥𝑑𝑥$

  1. If $j$ is even and $j\ge 2$, rewrite $\sec^𝑗 x = \sec^{𝑗−2}x\sec^2x$ and use $\sec^2x=\tan^2x+1$ to rewrite $\sec^{𝑗−2} x$ in terms of $\tan x$. Let $ u =\tan x$ and $ du =\sec^2 x$.

  2. If $k$ is odd and $𝑗\ge 1$, rewrite $\tan^𝑘𝑥\sec^𝑗𝑥=\tan^{𝑘−1}𝑥\sec^{𝑗−1}𝑥\sec 𝑥\ tan𝑥$ and use $\tan^2𝑥=\sec^2𝑥−1$ to rewrite $\tan^{𝑘−1}𝑥$ in terms of $\sec 𝑥$. Let $𝑢=\sec 𝑥$ and $𝑑𝑢=\sec 𝑥\tan 𝑥𝑑𝑥$. (Note: If $𝑗$ is even and $𝑘$ is odd, then either strategy 1 or strategy 2 may be used.)

  3. If $𝑘$ is odd where $𝑘\ge 3$ and $𝑗=0$, rewrite $\tan^𝑘𝑥=\tan^{𝑘−2}𝑥\tan^2𝑥=$ $\tan^{𝑘−2}𝑥(\sec^2𝑥−1)=\tan^{𝑘−2}𝑥\sec^2𝑥−\tan^{𝑘−2}𝑥$. It may be necessary to repeat this process on the $\tan^{𝑘−2}𝑥$ term.

  4. If $𝑘$ is even and $𝑗$ is odd, then use $\tan^2𝑥=\sec^2𝑥−1$ to express $\tan^𝑘𝑥$ in terms of $\sec 𝑥$. Use integration by parts to integrate odd powers of $\sec 𝑥$.

Reduction formulas

  1. $\int \sec^n xdx=\frac{1}{n-1}\sec^{n-2}x\tan x+\frac{n-2}{n-1}\int \sec^{n-2}xdx$, $n$​ is odd. Verified by applying integration by parts.
  2. $\int \tan ^n xdx=\frac{1}{n-1}\tan ^{n-1}x-\int\tan^{n-2}x dx$, $n$ is odd.

Method of Substitution

  1. The original integrand (in $g(x)dx$ or $h(t)dt$ … ) can be expressed as $f(u)\,du$.
  2. Usually $g(x)$ and $h(t)$ coule be a mess, but it is much easier to find the anti-derivative of $f(u)$.

Jacobian and Jacobian Matrix

Suppose $f$: $R_n \rightarrow R_m$ is a function such that each of its first-order partial derivatives exist on $R_n$.
Jacobian matrix is a matrix of partial derivatives. The Jacobian matrix of $f$ is defined to be an $m \times n$ matrix, denoted by $\mathbf{J}$, whose $(i,j)$ th entry is $\mathbf{J}_{ij}=\frac{\partial f_i}{\partial x_j}$.

Jacobian is the determinant of the Jacobian matrix.
The main use of Jacobian is found in the transformation of coordinates. It deals with the concept of differentiation with coordinate transformation.

假设$F:R_n→R_m$ 是一个从欧式 $n$ 维空间转换到欧式 $m$ 维空间的函数。这个函数由$m$个实函数组成：$ y_1=f_1(x_1, \ldots, x_n), \ldots, y_m=f_m(x_1,\ldots, x_n)$.
这些函数的偏导数(如果存在)可以组成一个 $m$ (dimension of $y$) 行 $n$ (dimension of $x$) 列的矩阵，这就是所谓的雅可比矩阵

\[\mathbf{J} = \begin{bmatrix} \frac{\partial \mathbf{y}}{\partial x_1} & \cdots & \frac{\partial \mathbf{y}}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \nabla^Tf_1 \\ \vdots \\ \nabla^Tf_m \end{bmatrix} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \cdots & \frac{\partial y_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_m}{\partial x_1} & \cdots & \frac{\partial y_m}{\partial x_n} \end{bmatrix}_{m\times n}\]

$\nabla^Tf_i$ the transpose (row vector) of the gradient of the $i$-th component of $f$. $\nabla^Tf_i$ 也叫做梯度函数的转置。
The Jacobian matrix can be also written as

\[\begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}_{m\times n}\]

此矩阵表示为：$J_F(x_1,\cdots ,x_n)$，或者: $\frac{\partial (y_1,\ldots,y_m)}{\partial (x_1, \ldots ,x_n)}$ or $\frac{\partial (f_1,\ldots,f_m)}{\partial (x_1, \ldots ,x_n)}$

  • The $i$-th row contains the derivative of the $i$-th components of $y_i$ with respect to all variables, denoted $\frac{\partial f_i}{\partial x}$.
  • The $k$-th column contains the all $m$ components of $f$ with respect to the $k$-th variable, denoted $\frac{\partial f}{\partial x_k}$.

当 $m=n$ 时，我们可以想象有6个函数，每个函数对应着有6个变量。那么针对每个输入变量 $x_i$，就会能够得到对应的 $y_i$

\[\begin{align*} y_1 &= f_1(x_1,x_2,x_3,x_4,x_5,x_6) \\ y_2 &= f_2(x_1,x_2,x_3,x_4,x_5,x_6) \\ y_3 &= f_3(x_1,x_2,x_3,x_4,x_5,x_6) \\ y_4 &= f_4(x_1,x_2,x_3,x_4,x_5,x_6) \\ y_5 &= f_5(x_1,x_2,x_3,x_4,x_5,x_6) \\ y_6 &= f_6(x_1,x_2,x_3,x_4,x_5,x_6) \end{align*}\]

因此 $y_i$ 的导数可以被写成

\[\mathrm{d} {y_i} = \frac{\partial f_i}{\partial x_1}{\mathrm{d} x_1} + \frac{\partial f_i}{\partial x_2}{\mathrm{d} x_2}+\frac{\partial f_i}{\partial x_3}{\mathrm{d} x_3}+\frac{\partial f_i}{\partial x_4}{\mathrm{d} x_4}+\frac{\partial f_i}{\partial x_5}{\mathrm{d} x_5}+\frac{\partial f_i}{\partial x_6}{\mathrm{d} x_6}\]

因此结合上面的方程，我们可以将上面的方程写为向量的形式：

\[{\mathrm{d} Y} = \frac{\partial F}{\partial X}{\mathrm{d} X}\]

函数$F$对于$X$的偏导数矩阵，就被称为雅可比矩阵 (Jacobian Matrix)。

Derivative vs. Gradient

Vector-by-scalar

The derivative of a vector $\mathbf {y} ={\begin{bmatrix}y_{1}&y_{2}&\cdots &y_{m}\end{bmatrix}}^{\mathsf {T}}$ by a scalar $x$ is is written as

\[{\frac {\partial \mathbf {y} }{\partial x}}={\begin{bmatrix}{\frac {\partial y_{1}}{\partial x}}\\{\frac {\partial y_{2}}{\partial x}}\\\vdots \\{\frac {\partial y_{m}}{\partial x}}\\\end{bmatrix}}.\]

In vector calculus the derivative of a vector $y$ with respect to a scalar $x$ is known as the tangent vector of the vector $y$, $\frac{\partial \mathbf{y}}{\partial x}$. Notice here that $y$: $\mathbb{R}^1 \rightarrow \mathbb{R}^m$.

Scalar-by-vector

The derivative of a scalar $y$ by a vector $\mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}^{\mathsf {T}}$ , is written (in numerator layout notation) as

\[{\frac {\partial y}{\partial \mathbf {x} }}={\begin{bmatrix}{\dfrac {\partial y}{\partial x_{1}}}&{\dfrac {\partial y}{\partial x_{2}}}&\cdots &{\dfrac {\partial y}{\partial x_{n}}}\end{bmatrix}}.\]

In vector calculus, the gradient of a scalar field $f$ in the space $\mathbb{R}^n$ (whose independent coordinates are the components of $x$) is the transpose of the derivative of a scalar by a vector.

\[\nabla f={\begin{bmatrix}{\frac {\partial f}{\partial x_{1}}}\\\vdots \\{\frac {\partial f}{\partial x_{n}}}\end{bmatrix}}=\left({\frac {\partial f}{\partial \mathbf {x} }}\right)^{\mathsf{T}}\]

Gradient:

https://www.youtube.com/watch?v=QQPz3eXXgQI&t=452s

Reference:

https://loopvoid.github.io/2018/04/28/Jacobian%E7%9F%A9%E9%98%B5%E4%B8%8EHessian%E7%9F%A9%E9%98%B5%E4%B8%8E%E6%9C%80%E5%B0%8F%E4%BA%8C%E4%B9%98/
https://en.wikipedia.org/wiki/Matrix_calculus