Notation

$\mathbb{E}_Y$ and $\mathrm{Var}_Y$ denote expectation over $Y$ and variance over $Y$.

$\text{Pr}(.)$ and $\mathbb{P}(.)$ denote the probability of an event.

Blackboard bold 黑板粗体 (\mathbb) is often used to denote sets of numbers, e.g. $\mathbb{N}$, $\mathbb{Z}$, $\mathbb{Q}$, $\mathbb{R}$, $\mathbb{C}$, $\mathbb{H}$, $\mathbb{O}$, or a general field $\mathbb{F}$ or $\mathbb{K}$, and in probability to denote expectation of a random variable $\mathbb{E}(X)$ , written as \mathbb{E}(X), or probability of an event $\mathbb{P}(E)$, written as \mathbb{P}(E).

  • $\mathbb{N}$ denotes the set of all natural numbers: $\{1,2,3,\dots\}$.
  • $\mathbb{Z}$ denotes the set of all integers: $\{\dots, -3,-2,-1,0,1,2,3,\dots \}$.
  • $\mathbb{Q}$ denotes the set of all rational numbers. The sets of all fractions $\frac{a}{b}$ where $a$ and $b$ are integers and $b\ne 0$

  • $\mathbb{R}$ denotes the set of all real numbers. This includes things like $\pi, \sqrt{2}, \dots$

  • $\forall$ (\forall) means for all (or for every).
  • $\exists$ (\exists) means there exists.

  • $\not\exists$ (\not\exists) means there does not exist.

  • $E\left[\abs{Z_t}\right]<\infty$ means the expected value of the absolute value of $Z_t$ is finite.

Indicator function: $\mathbb{1}(\text{condition})$ or $I(\text{condition})$

\[\mathbb{1}(\text{condition}) = \begin{cases} 1 & \text{condition is true} \\ 0 & \text{condition is false} \end{cases}\]

There are two standard ways to describe a set:

  • The extensional method simply lists out all the elements of the set. For example $S = \{0, 2, 4, 6, 8, 10\}$.

  • The intensional method describes a set by listing the common properties of the elements of the set. For example,

    \[S = \{n \in \mathbb{Z} \; | \; n \; \textrm{is even }, 0 \leq n \leq 10\}.\]

    By putting $n\in \mathbb{Z}$ before the vertical bar, we know that we only concern with integers in this set. This is called the universe. We read the first brace as “the set of all” and the vertical bar as “such that”. So the expression is read as the set of all integer $n$ such that $n$ is even which is greater than or equal to 0 and less than or equal to 10.

    The general syntax of the intensional method is \(\{\textrm{expression} \in \textrm{universe} \; | \; \textrm{rule}\}.\)

Sometimes, you see people use colon (:) to define sets, e.g., $\{x: x\in A\}.$ This is equivalent to $\{x\mid x\in A\}.$ There are pros and cons for using either convention.

  • With :, it confuses with sets of maps

    \[\{f: f: \R \to \C \text{ with} f(6)=24\} .\]

    In this case, it is easier to read with bar separator

    \[\{f\mid f: \R \to \C \text{ with} f(6)=24\} .\]

  • With |, it confuses with norms and conditional statements, risking overloading bars.

    \[\{A \subset X \mid \P(B \mid A) > 0.42\} \quad\text{vs}\quad \{A \subset X : \P(B \mid A) > 0.42\}\] \[\{A \subset X \mid \P(B \mid A) > 0.42\} \quad\text{vs}\quad \{A \subset X : \P(B \mid A) > 0.42\}\]

    In this case, it is better to use colons.

In any given problem, the set containing all possible elements of interest is called the universe, universal set, or sample space, often denoted as $S$ or $\Omega$.

  • $\setminus$ means remove from a set. Given two sets $S$ and $T$, $S\setminus T$ is used to denote the set $\{x\mid x\in S \text{ and } x\notin T\}.$ For example $\{1,2,3\} \setminus \{3,4,5\} = \{1,2\}.$ Often we assume $T\subseteq S$ as well. Sometimes a minus sign is used, e.g., $X-T.$

A random experiment is completely characterized by:

\[\{ S, \mathcal F(S), \mathbb P(.) \}\]

where

  • $S$ is the sample space;
  • $\mathcal F(S)=[E_1, E_1, \ldots, ]$ is the event space; and
  • $\mathbb P(.): \mathcal F(S) \rightarrow [0,1]$ is the probability measure that assigns probability to each of the event in the event space.

If $\P(A)=1,$ we say $A$ occurs almost surely.

Sometimes you see a sphere denoted $\mathbb{S}$ or a torus denoted $\mathbb{T}$.

Mathematical calligraphic font or script letters 花体 (\mathcal), uppercase only, font for set, categories, and sheaves (集合，拓扑空间，层).

  • $\mathcal L$（\mathcal L）常用来表示损失函数; log likelihood function;
  • $\mathcal D$（\mathcal D）表示样本集;
  • $\mathcal N$（\mathcal N）常用来表示高斯分布; normal distribution;
  • $\ell$（\ell）：用于和 $l$ 和 数字 1 相区分。
  • $\mathcal{T}$ (\mathcal{T}) used to denote topological spaces.

Mathematical roman \mathrm (or \text). Used in ordinary differential equations, such as $\displaystyle \frac{\mathrm dx}{\mathrm dy}$ or variance $\mathrm{Var}$.

Mathematical sans serif \mathsf. Used in expectations, such as $\mathsf E(X)$.

Usually the font command works only on the following letter. If you want the font to apply to an entire expression, enclose the expression with braces {}.

$\indep$ independence

$\perp$ uncorrelated

:= and $\triangleq$ are used to define a variable.

$\nabla:=\begin{pmatrix}\frac{\partial}{\partial x_1} \cr \vdots \cr \frac{\partial}{\partial x_n} \end{pmatrix}$, called “nabla symbol” or “nabla operator” (\nabla), commonly used in vector analysis and multivariate calculus. E.g., Let $f(x_1, x_2)=x_1^3$, $\mathbb{R}^2 \rightarrow \mathbb{R}$, then the gradient of $f$ is $\nabla f(x_1, x_2) = \begin{pmatrix}\frac{\partial f}{\partial x_1} \cr \frac{\partial f}{\partial x_2} \end{pmatrix} = \begin{pmatrix} 3x_1^2 \cr 0 \end{pmatrix} $.

Upper- and lower-case letters

Vectors are lowercase and matrices are uppercase symbols. Both vectors and matrices are written in bold-italic.

  • Vector $\boldsymbol a$, $\boldsymbol b, \boldsymbol c$ are produced by \mathbfit a or \boldsymbol a… ; vectors can also be denoted by bold face Greek lowercase letters: $\boldsymbol{\alpha, \ldots \omega}$

  • Matrices $\boldsymbol A, \boldsymbol B, \boldsymbol C$ by \mathbfit A or \boldsymbol A … ; matrices can also be denoted by bold face Greek uppercase letters: $\boldsymbol{\Gamma, \ldots, \Theta}$

    • $\bA = [a_{ik}] = [\bA]_{ik}$ to show the $(i,k)$ components of matrix $\boldsymbol A$.

    • $\ba_k,$ $\ba_l,$ $\ba_m,$ denote column $k,$ $l,$ or $m$ of the matrix $\bA.$

\[\underset{n\times K}{\bA} = \begin{bmatrix} \ba_1 & \cdots & \ba_l & \cdots & \ba_K \end{bmatrix}\]
  • $\ba_i,$ $\ba_j,$ $\ba_s,$ or $\ba_t,$ denote the column vector formed by the transpose of row $i,$ $j,$ $t,$ or $s$ of matrix $\bA.$ Thus $\ba_i’$ is row $i$ of $\bA.$
\[\underset{n\times K}{\bA} = \begin{bmatrix} \ba_1' \\ \vdots \\ \ba_i' \\ \vdots \\ \ba_n' \\ \end{bmatrix}\]

  • Sets are denoted by capital letters, optionally in calligraphy, $A, B, C, \ldots$

  • Random variables are uppercase italic Latin letters $X, Y, X$. Lower case letters $x, y,z$ mean values of random variables. Sometimes, $X_i$ also denotes a value. If $X$ is a RV, then $X$ is written in words, and $x$ is given as a number.
    • Sample data use lowercase.
    • Population data use uppercase.
  • Use Greek letters $\boldsymbol\theta, \boldsymbol\phi$ for parameters or $\alpha, \beta, \gamma$ for hyperparameters.
  • Error terms are denoted by $\epsilon, \varepsilon, \eta, \xi, \zeta$.
  • Variance-covariance matrices: $\boldsymbol{\Omega}, \boldsymbol{\Sigma}, \boldsymbol{V}, \boldsymbol{G}$.

  • $\text{aVar}[.]$ denotes the asymptotic variance operator.

  • The letters $f$, $g$, and $h$ are often used to represent functions.

  • $f(x) \approx g(x)$ (\approx) if the two functions are approximately equal in some sense depending on the context.
  • $f(x) \propto g(x)$ (\propto) If $f(x)$ is proportional to $g(x)$ we write.
  • $f(x) = O(g(x))$ We say that “$f(x)$ is at most of order $g(x)$,” if $\vert f(x)/g(x)\vert$ is bounded from above in some neighborhood of x = c (possibly c = ±∞).
  • $f(x) = o(g(x))$ we say that “$f(x)$ is of order less than $g(x)$,” if $f(x)/g(x)$→ 0 when $x \rightarrow c$.
  • $f(x)\sim g(x)$ (\sim) if $f(x)/g(x) \rightarrow 1$ when $x \rightarrow c$. The two functions are then said to be “asymptotically equal”. Notice that when $f(x)$ and $g(x)$ are asymptotically equal, then $f(x)\approx g(x)$ and also $f(x) = O(g(x))$, but not vice versa.

Reference: https://www.principlesofeconometrics.com/poe5/writing/abadir_magnus.pdf

crit pt: critical point.

cts: continuous.

def'n: definition.

cont'd: continued.

iff: if and only if.

GWN: Gaussian White Noise.

i.i.d.: independent and identically distributed

Thm: theorem.

viz.: namely, that is to say.

Q.E.D or QED: Latin words to indicate this is the end of a mathematical proof. At the beginning, you simply write Proof:.

NB: Latin phrase meaning “note well” or “pay special attention.”

Ceteris paribus: Latin phrase that generally means “all other things being equal.”

axiom or postulate: a fundamental assumption that is accepted without proof.

theorem: a statement that has been proven to be true based on axioms and other theorems.

preposition: a theorem of less importance, or one that is considered so elementary or immediately obvious, that it may be stated without proof.

lemma: an “accessory preposition” - a preposition with little applicability outside its use in a particular proof. Over time a lemma may gain in importance and be considered a theorem, though the term “lemma” is usually kept as part of its name.

corollary: is a theorem of less importance which can be readily deduced from a previous, more notable statement. A corollary may also be a restatement of a theorem in a simpler form, or for a special case.

罗马数字共有7个，即 Ⅰ (1)、Ⅴ(5)、Ⅹ(10)、Ⅼ(50)、Ⅽ(100)、Ⅾ(500) 和Ⅿ(1000)。

  • 重复数次：一个罗马数字重复几次，就表示这个数的几倍。
  • 从小到大，表示大数字减小数字。E.g. IV(4).
  • 从大到小，表示大数字加小数字。E.g. VI(6).
  • 常见罗马数字 IV(4), V (5), Ⅵ (6), Ⅶ (7), ⅦI (8), IX(9).

domain 定义域

range 值域

summand 被加数

reciprocal (multiplicative inverse) 倒数

normal vector 法向量

direction vector 方向向量

recursive substitution 迭代

counterexample 反例

$>$ greater than, larger than 大于

$<$ less than, smaller than 小于

$\geq$ greater than or equal to 大于等于

$\leq$ less than or equal to 小于等于

$\approx$ approximately equal to 约等于

Inequality 不等式 (大于/小于)

SS: sum of squares

\[SS=\sum_i (X_i-\overline{X})^2\]

  • Multiplying or dividing both sides by a positive number leaves the inequality symbol unchanged.

  • Multiplying or dividing both sides by a negative number reverses/ flips the inequality. This means $<$ changes to $>$, and vice versa.

Natural experiment (or a quasi-experiment) occurs when some exogenous event – often a change in government policy – changes the environment in which individuals, families, firms, or cities operate.

A natural experiment always has a control group, which is not affected by the policy change, and a treatment group, which is thought to be affected by the policy change. Unlike a true experiment, in which treatment and control groups are randomly and explicitly chosen, the control and treatment groups in natural experiments arise from the particular policy change.

Random Variables

Given a random experiment with sample space $S$, a random variable $X$ is a set function that assigns one and only one real number to each element $s$ that belongs in the sample space $S$.

The set of all possible values of the random variable $X$, denoted $x$, is called the support, space, or range, of $X$.

Sample and population

  • DGP (data generating process) generates the data that we observe.
  • Any quantity, the calculation of which requires one to know the DGP, is a population quantity

Degenerate distribution: sometimes called a constant distribution, is a distribution of a degenerate random variable — a constant with probability of 1.
In other words, a random variable $X$ has a single possible value. E.g., a weighted die (or one that has a number 6 on all faces) always lands on the number six, so the probability of a six is 1, i.e., $P_X(X=6)=1$.

Spherical disturbances: homoskedasticity and non-autocorrelation

Nonspherical disturbances: heteroskedasticity and autocorrelation

Average ($\overline{X}$) usually denotes sample, expected value ($E[X]$) and mean ($\mu$) denote population.

Write a sequence of calculations using the “two-column method”. This method is good for simple derivations in homework, but is not suitable for a research paper, where calculations should be integrated into the flow of the text, using both words and symbols to provide a smooth, narrative-driven explanation.

\[\begin{aligned} & \quad & 3^{2x} - 2 (3^x) &= -1 \\ & \rightarrow & (3^x)^2 - 2 (3^x) + 1 &= 0 &\quad & \text{(rewrite this equation in terms of $3^x$)} \\ & \rightarrow & (3^x-1)^2 &=0 &\quad & \text{(factor)} \\ & \rightarrow & 3^x &=1 &\quad & \text{(zero factor property)} \\ & \rightarrow & x &=0 \end{aligned}\]

Critical values The $\alpha-$level critical value is the value $x_\alpha$ such that

\[F(x_\alpha)=P(X\le x_\alpha)=1-\alpha\]

where $F$ is the cdf of the random variable $X$. In other words, the probability of $X>x_\alpha$ is $\alpha$.

Critical values can be obtained by taking the inverse of the cdf, i.e.,

\[x_\alpha = F^{-1}(1-\alpha) \,.\]

Note that sometimes the subscript denotes the probability of the quantile directly, that is,

\[x_{1-\alpha} = F^{-1}(1-\alpha) \,.\]

You can tell from the context.

There are standard notations for the upper critical values of some commonly used distributions in statistics:

  • $z_\alpha$ or $z(\alpha)$ for the standard normal distribution
  • $t_{\alpha, v}$ or $t(\alpha, v)$ for the t-distribution with $v$ degrees of freedom
  • $\chi_{\alpha, v}^2$ or $\chi^2 (\alpha, v)$ for the $\chi-$squared distribution with $v$ degrees of freedom
  • $F_{\alpha, v_1, v_2}$ or $F (\alpha, v_1, v_2)$ for the $F-$distribution with $v_1$ and $v_2$ degrees of freedom

Asymmetric deviations

  • $(x-\bar{x})^+$ deviation above the mean. $(x - \bar{x})^+ = \max(0, {\color{#008B45} x - \bar{x}})$, or
\[(x - \bar{x})^+ = \begin{cases} x - \bar{x}, & \text{if } x > \bar{x} \\ 0, & \text{otherwise} \end{cases}\]
  • $(x-\bar{x})^-$ deviation below the mean. $(x - \bar{x})^- = \max(0, {\color{#008B45}\bar{x} - x})$, or
\[(x - \bar{x})^- = \begin{cases} \bar{x} - x, & \text{if } x < \bar{x} \\ 0, & \text{otherwise} \end{cases}\]

A more concise expression:

\[\begin{split} z^+ &= z I(z\ge 0) \\ z^- &= -z I(z<0) \\ \end{split}\]
$z$ $z^+$ $z^-$
3 3 0
0 0 0
-2 0 2
  • $z^+$ is the positive part of $z$
  • $z^-$ is the negative part of $z$, but made positive, so $z^-\ge 0.$

How to spell out numbers

  • 两位数的英文写法 (21-99): write the tens part, then, put a hyphen (-), and write the ones part. E.g., 68 (sixty-eight).

  • 三位数的英文写法 (100-999): write the hundreds part. Then write the tens part, hyphen, then the ones part. E.g., 341 (three hundred forty-one).

  • hundred, thousand, million etc. in numbers are used as adjectives. So they are not changed to plural numbers by adding -s to them.

  • Do not use “and” in whole numbers.

    The word “and” is not written with whole numbers. You might say “four hundred and fifty,” but do not write the “and.” For example:

    • 3,567 (three thousand five hundred and sixty-seven wrong ❌)
    • 3,567 (three thousand five hundred sixty-seven correct ✅)

  • Use “and” for the decimal point.

    If the numbers after the decimal point are not said as figures, then use “and” instead of “point.” E.g.,

    • $3,567.65 (three thousand five hundred sixty-seven dollars and sixty-five cents correct ✅)
    • 234.2 (two hundred thirty-four and two tenths correct ✅)

    If numbers after the decimal point being said as figures, use “point.”

    • 234.2 (two hundred thirty-four point two correct ✅)
    • 44,120.42 (forty-four thousand one hundred twenty point four two correct ✅)

commutative property: 交换律

associative property: 结合律

Fractions in word

  • Use hyphen between the numerator and the denominator.
    • When the numerator or the denominator includes a hyphen already, then the hyphen between the numerator and the denominator is often dropped for style purposes. E.g., $3/35$ (three thirty-fifths)
  • Numerator is in cardinal (one, two, three 基数词); denominator is in ordinal (first, second, third 序数词).
  • E.g., $1/2$ (one-half), $2/3$ (two-thirds), $3/11$ (three-elevenths), $3 5/7$ (three and five-sevenths)

Decrease/increase a negative number: “increase” means move to the right (become “more positive”) and “decrease” means move to the left (become “more negative”).

  • Decreasing a nagative number means move away zero; i.e., add a negative number to it. E.g, decreasing –5 by 3 results in –8; decreasing –3 by 2 results in –5.
  • Increaseing a negative number means move to zero; i.e., add a positive number to it. E.g, increasing –5 by 3 results in –2; increasing -3 by 2 results in –1.

But there are different answers:

Positive and negative numbers are “directed numbers.” In terms of “absolute value,” the direction no longer applies. The decreasing of a negative number is the same as the decreasing value of a positive number —toward zero.

Compare negative numbers: the one to the left on the number line is smaller.

  • –3 is less than –1 because –3 is to the left of –1
  • –5 is less than –3 because –5 is to the left of –3

Elementary arithmetic

四则运算

$a+b=c$: a plus b equals c (plus是介词).

$a-b=c$: a minus b equals c (minus是介词); b substracted from a leaves c.

$a\times b=c$: a times b equals c (times是介词); a multiplied by b is c.

$a\div b=c$: a divided by b equals c.

$1/x$: the reciprocal of x.

$3:5$: three to five.

Polynomial and Exponential

多项式与指数

A standard polynomial is one where the highest degree is the first term, and the subsequent terms are arranged in descending order of the powers or the exponents of the variables followed by constant values.

  • The number multiplied by a variable is called the “coefficient”.
  • The number without any variable is called a “constant”.

$A^B$: $A$ is called the base (幂底数), $B$ is exponent (幂指数).

Polynomials, $x$ in the base. constant ($x^0$), linear ($x$), quadratic ($x^2$), cubic ($x^3$), quartic terms ($x^4$).

$x^4$ read as $x$ to the 4th or the quartic term.

$2^{16}$ is read as “2 to the 16th power” or “2 to the power of 16” in formal speech. Commonly, a ellipsis of the first expression is used “2 to the 16th” (ordinal) or “2 to the 16” (w/o ordinal).

For example, a polynomial $x^{109} + 9x^5 − 2x^2$ is most likely pronounced:

x to the hundred and nine plus nine x to the fifth minus two x squared.

二项式
Binomial (based on terms) or quadratic polynomial (based on degrees)
A binomial is a polynomial with two terms. (只有两项的多项式)

因式分解，或多项式因式分解（Polynomial Factorization），是把一个多项式分解为两个或多个的因式的过程。在这个过后会得出一堆较原式简单的多项式的积。例如单元多项式 $x^{2}-1^{2}$ 可被因式分解为 $\left(x+1\right)\left(x-1\right)$。

  • Collect terms: 合并同类项
  • Collect like powers of $L$: 合并 $L$ 的同次幂，e.g., $aL^2+bL^2=(a+b)L^2$

Exponential $x$ in the exponent.

If there is a variable in the exponent, the ordinal is not used. $x^y$ is read as “x to the y”. The -th is dropped.

开方 ($n$th root)

$\sqrt{9}$: the square root of $9$.

$\sqrt[3]{8}$: the cube root of $8$.

$\sqrt[n]{b}$: the $n$-th root of $b$.

$e^x$: take the exponential of $x$ or apply the exponential function to $x$.

Scientific e notation: Because superscript exponents like $10^7$ can be inconvenient to display or type, the letter “E” or “e” (for “exponent”) is often used to represent “times ten raised to the power of”, so that the notation m E n for a decimal significand m and integer exponent n means the same as $m \times 10^n$. E.g., $6\times 10^7$ can be written as 6e7.

  • e+n or en: $10^n$ (+ can be omitted for positive exponent)
  • e-n: $10^{-n}$

Note that e notation is often used in computer programs display. It is not suggested for published documents.

对数 (logarithm)

$\log_b x$: the logarithm of $x$ to base $b$.

$\log x, \ln x, \log_ex$: the natural logarithm of $x$.

$\lg x, \log_{10}x$: the common logarithm of $x$.

$\text{lb} x, \log_2x$: the binary logarithm of $x$.

1 micrometer = $10^{-6}$ meter

1 nanometer = $10^{-9}$ meter

$a_1$: a (sub) one.

$\varepsilon_{ijk}$: epsilon (sub) ijk.

$a^i$: a super $i$.

Double Summation

We can interchange the order of double summation.

\[\sum_{i,j} a_jb_j = \sum_{i=1}^k\sum_{j=1}^m a_ib_j = \sum_{j=1}^m\sum_{i=1}^k a_ib_j\]

Distributive law for multiplication (from product of sums to double sums)

\[\left( \sum_{i=1}^k a_i \right) \cdot \left( \sum_{j=1}^m b_j \right) = \sum_{i=1}^k \left(\sum_{j=1}^m a_ib_j\right)\]

Arithmetic Sequence/Progression 等差数列

$a_1, a_2, …, a_n$ has common difference $d$, $n$ is the number of terms. Some useful formulas:

  • the $n$-th term: $a_n=a_1+(n-1)\,d$
  • sum of first $n$ terms: $S_n=\frac{(a_1+a_n)\,n}{2}=na_1+\frac{n(n-1)}{2}\,d$
  • number of terms: $n=\frac{a_n-a_1}{d}+1$
  • common difference: $d=\frac{a_n-a_1}{n-1}$

Geometric Sequence/Progression 等比数列

$a_1, a_2, …, a_n$ has common ratio $q$.

  • $a_n=a_1\cdot q^{n-1}$
  • $\displaystyle S_n= \frac{a_1(1-q^n)}{1-q}$

(Backward) recursion: (逆向) 递归迭代

  • Finite: something has an end.
  • Infinitely: till the end of time. E.g., The stars will infinitely be present in space.
  • Definite: there is a clear end.

  • Indefinitely: means you don’t know when something is going to end. E.g., Due to Covid-19, the schools have been closed indefinitely.

  • Filtering: The operation of taking a weighted average of (possibly infinitely many) successive values of a process. E.g.,
\[y_t = \mu + \sum_{j=0}^\infty \phi_j\varepsilon_{t-j}\]

Distribution Functions

Visualization tool: https://seeing-theory.brown.edu/probability-distributions/

Plot a function: https://www.desmos.com/calculator

Geometry

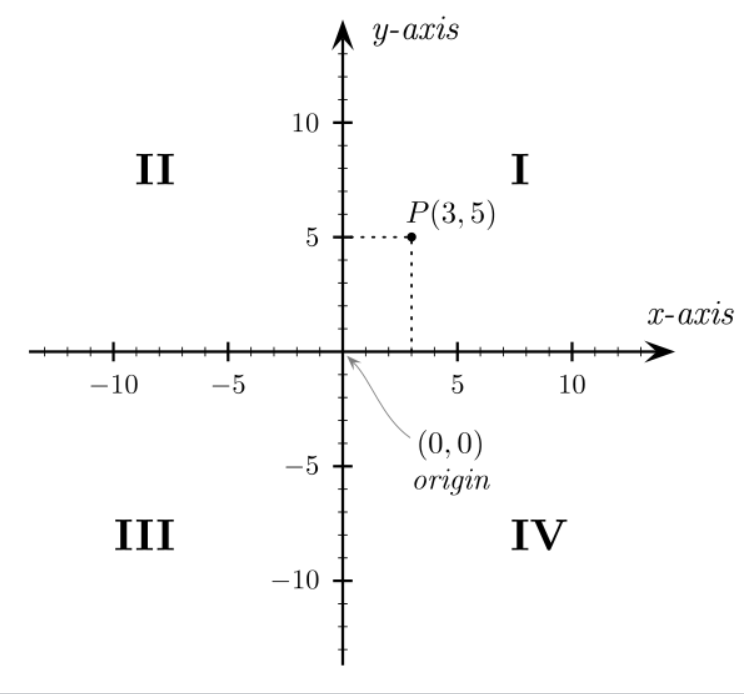
Quadrant (plane geometry)

The axes of a two-dimensional Cartesian system divide the plane into four infinite regions, called quadrants, each bounded by two half-axes.

  • the numbering goes counter-clockwise starting from the upper right (“northeast”) quadrant.

quadrant geometry

orthographic projection (正射投影): top view, front view, (right) side view.

锐角 acute angel
钝角 obtuse angel
直角 right angel

complementary angel 互余角 $\alpha+\beta=\frac{\pi}{2}$.

supplementary angel 互补角 $\alpha+\beta=\pi$.

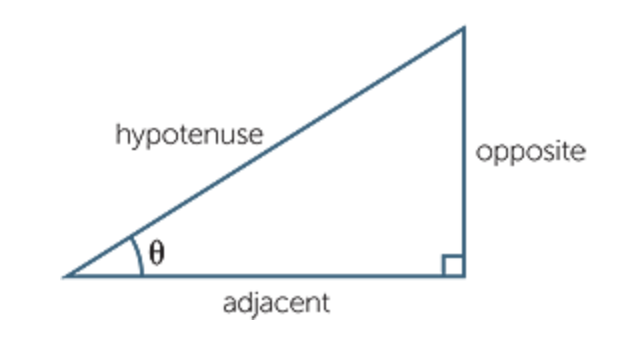
triangel

斜边 hypotenuse /haɪˈpɑːtənuːs/
邻边 adjacent side
对边 opposite side

Pythagoras’ /pəˈθægərəs/ or Pythagorean /pəˌθæɡəˈriən/ theorem 勾股定理

Law of Cosine: tells the length of the 3rd side of a triangle if we know 2 sides and the angle between them.

\[\begin{align*}c^2=a^2+b^2-2ab\cos\theta\end{align*}\]

circumference /sərˈkʌmfərəns/ 周长

trapezoid 梯形 $A=\frac{(a+b)}{2}\cdot h$. (上底 + 下底) $\times$ 高/2.

parallelogram /ˌpærəˈleləɡræm / 平行四边形

parallelepiped /ˌpærəˌleləˈpaɪˌpɪd / 平行六面体 (倾斜长方体)

tetrahedron /ˌtetrəˈhiːdrən/ 四面体, also called “tiangular pyramid”, 三角锥, is a polyhedron composed of four triangular faces.

polyhedron 多面体
cube 正方体
cuboid 长方体

sector 扇形
已知弧长 $A=\frac{1}{2}l\cdot r$。 $l$ 为扇形弧长，$r$ 为半径。与三角形面积类比，$\frac{1}{2}$底$\times$高，半径可看作底，弧长看作高。

已知圆心角 $A=\frac{n}{360}\pi r^2=\frac{1}{2}\theta\cdot r^2$。$n$单位为度数degree， $\theta$ 为圆心角，单位为弧度radian。

  • 度数弧度转换公式：$\frac{n}{180}\pi=\theta$。

  • 弧长公式：$l=\theta \cdot r$ (圆心角弧度 $\times$ 半径)。

    圆周长 $C=2\pi r$，弧长 $l=\frac{\theta}{2\pi}\cdot C=\frac{\theta}{2\pi}\cdot 2\pi r=\theta r$。

Volume of a sphere (ball) $V=\frac{4}{3}\pi r^3$, $r$ is radius. Surface $S=4\pi r^2$.

secant line 割线
tangent line 切线

直线方程的各种形式

  1. 一般式: $Ax+By+C=0$
    斜率: $k=-\frac{A}{B}$
    法向量: $\overrightarrow{\textbf{n}}=(A,B)$
    方向向量: $\overrightarrow{\textbf{a}}=(B,-A)$
  2. 点斜式: $y-y_0=k(x-x_0)$
    点斜式是由一个定点 $P(x_0,y_0)$ 和斜率 $k$ 确定的直线方程。
    斜率: $k$
    法向量: $\overrightarrow{\textbf{n}}=(k,-1)$
    方向向量: $\overrightarrow{\textbf{a}}=(1,k)$
  3. 斜截式: $y=kx+b$
    斜截式是由斜率 $k$ 和 $y$ 轴上的截距 $b$ 确定的直线方程。
    斜率: $k$
    法向量: $\overrightarrow{\textbf{n}}=(k,-1)$
    方向向量: $\overrightarrow{\textbf{a}}=(1,k)$
  4. 两点式: $\displaystyle \frac{y-y_1}{y_2-y_1} = \frac{x-x_1}{x_2-x_1}$
    两点式是由已知的两个点 $(x_1,y_1)$, $(x_2,y_2)$ 确定的直线方程。
    斜率: $k = \frac{y_2-y_1}{x_2-x_1}$
    法向量: $\overrightarrow{\textbf{n}}=(y_2-y_1,x_1-x_2)$
    方向向量: $\overrightarrow{\textbf{a}}=(x_2-x_1,y_2-y_1)$
  5. 点向式: $\displaystyle \frac{y-y_0}{b} = \frac{x-x_0}{a}$
    点向式是由已知的定点 $P(x_0,y_0)$ 和方向向量 $\overrightarrow{\textbf{a}}=(a,b)$ 所确定的直线方程。
    斜率: $k = \frac{b}{a}$
    法向量: $\overrightarrow{\textbf{n}}=(b,-a)$
    方向向量: $\overrightarrow{\textbf{a}}=(a,b)$
  6. 参数式: $\left\{\begin{aligned}&x=x_0+at & \\ &y = y_0+bt & \end{aligned}\right.$
    这里的参数是$t$，是点向式的变式，也是由定点 $P(x_0,y_0)$ 和方向向量 $\overrightarrow{\textbf{a}}=(a,b)$ 所确定的直线方程。
    斜率: $k = \frac{b}{a}$
    法向量: $\overrightarrow{\textbf{n}}=(b,-a)$
    方向向量: $\overrightarrow{\textbf{a}}=(a,b)$
  7. 特别参数式: $\left\{\begin{aligned}&x=x_0+t\cos \alpha & \\ &y = y_0+t\sin \alpha & \end{aligned}\right.$
    这里的参数是 $t$，是参数式的特例，即以直线的倾角。
    斜率: $k = \tan \alpha$
    法向量: $\overrightarrow{\textbf{n}}=(\sin \alpha, -\cos \alpha)$
    方向向量: $\overrightarrow{\textbf{a}}=(\cos \alpha, \sin \alpha)$
  8. 点法式: $A(x-x_0)+B(y-y_0)=0$
    点向式是由已知的定点 $P(x_0,y_0)$ 和法向量 $\overrightarrow{\textbf{a}}=(a,b)$ 所确定的直线方程。
    斜率: $k = -\frac{A}{B}$
    法向量: $\overrightarrow{\textbf{n}}=(A,B)$
    方向向量: $\overrightarrow{\textbf{a}}=(B,-A)$

Reference: https://zhuanlan.zhihu.com/p/26263309

dot product vs. cross product

  • dot product is a scalar, used to calculate projection along a direction ($\vec{A}\cdot \hat{u}$ is the component of $\vec{A}$ along $\hat{u}$, ^ indicates a unit vector); determine if two vectors are orthogonal (if $\vec{A}\cdot\vec{B}=0$, then $\vec{A}\perp\vec{B}$);

    • The magnitude of the dot product is the same as the magnitude of one of them, multiplied by the component of one vector that is parallel to the other.
    \[\begin{align*} \vec{A}\cdot\vec{B} &= \sum_i a_ib_i \\ \vec{A}\cdot\vec{B} &= \vert\vec{A}\vert\vert\vec{B}\vert \cos\theta \\ \vec{A}\cdot\vec{A} &= \vert A\vert^2 \quad (\cos0=1) \end{align*}\]

  • cross product is a vector, used to 1) calculate area of parallelogram formed by two vectors; 2) get the normal vector; if $\vec{A}\times\vec{B}=0$, then $\vec{A}\parallel\vec{B}$ (parallel);

    • The magnitude of the cross product is the same as the magnitude of one of them, multiplied by the component of one vector that is perpendicular to the other.
    • If $\vec{A}\parallel\vec{B}$, no component is perpendicular to the other vector. Hence, the cross product is 0 although you can still find a perpendicular vector to both of these.
    \[\begin{align*} \vec{A}\times\vec{B} &=\vert\vec{A}\vert\vert\vec{B}\vert \sin\theta\cdot\vec{n},\; \vec{n} \textrm{ decided by right-hand rule.} \\ \vec{A}\times\vec{A}&=0 \quad (\sin0=0\textrm{, area of a line is 0}) \end{align*}\]

Geometric illustration:
https://math.stackexchange.com/a/1730547

Inner and Outer Product

If $X$ and $Y$ are random variables, then the inner product is given by

\[\langle X, Y\rangle = \E[XY]\]

and norm is given by $\Vert Y \Vert^2 = \langle Y, Y\rangle = \E Y^2.$

A random variable $S’$ is called a projection (or $L_2$-projection) of $Y$ onto $\Scal$ if $S’\in \Scal$ and

\[\E(Y-S')^2 \le \E(Y-S)^2 \quad \forall S\in \Scal.\]

In words, $S’$ is the projection of $Y$ onto $\Scal$ if its the best approximation of $Y$ in $\Scal$ in terms of mean squared error (MSE).

$\E[Y\mid X]$ is the function of $X$ that has the smallest possible MSE for predicting $Y.$ Thus $\E[Y\mid X]$ is the projection of $Y$ onto the set of random variables $\{h(X)\mid h \text{ is any real-valued function}\}.$

If $\boldsymbol{u}$ and $\boldsymbol{v}$ are column vectors with the same size, then $\boldsymbol{u}^T \boldsymbol{v}$ is the inner product; if $\boldsymbol{u}$ and $\boldsymbol{v}$ are column vectors of any size, then $\boldsymbol{u} \boldsymbol{v}^T$ is the outer product.

  • Inner product is a number;
  • Outer product is a matrix. Let $\boldsymbol{u}$ be $n\times 1$ and $\boldsymbol{v}$ be $m\times 1$, then $\boldsymbol{u} \boldsymbol{v}^T$ is $n\times m$.