Data Visualization

Study Objectives

Loads and prepares the California school dataset (CASchools) for analysis.
- Demonstrates how to visualize data using scatter plots, line charts, histograms, box plots.
- Explores expenditure per student across different grade spans.
- Investigates correlations between expenditure and other variables.
QQ plots to assess normality and interpret skewness and kurtosis in the data.
- Given a QQ plot, you should be able to identify how does the distribution compare to normal: positively skewed, negatively skewed, has fat tails, or thin tails.

1 Descriptive Analysis and Data Visualization with `CASchools`

Data visualization is a powerful tool for understanding patterns, relationships, and distributions in datasets. In this session, we will explore the California Schools dataset using various visualization techniques including histograms, box plots, scatter plots, and Q-Q plots. These visualizations help us answer important questions about educational spending, student performance, and the relationships between various school characteristics.

1.1 Dataset Overview

The following prints the first and last 5 rows of the dataset, together with data types of each column:

# load packages and dataset
pkgs <- c("tidyverse", "moments", "data.table", "ggsci")
missing <- setdiff(pkgs, rownames(installed.packages()))
if (length(missing) > 0) install.packages(missing)
invisible(lapply(pkgs, function(pkg) suppressPackageStartupMessages(library(pkg, character.only = TRUE))))
f_name <- "https://raw.githubusercontent.com/my1396/FIN5005-Fall2025/refs/heads/main/data/CASchools_test_score.csv"
cas <- read_csv(f_name, 
  col_types = cols(
    county = col_factor(), # read as factor
    grades = col_factor()
  ))

The following prints the first and last 5 rows of the dataset, together with data types of each column:

cas %>% as.data.table()

     district                          school      county grades students
        <num>                          <char>      <fctr> <fctr>    <num>
  1:    75119              Sunol Glen Unified     Alameda  KK-08      195
  2:    61499            Manzanita Elementary       Butte  KK-08      240
  3:    61549     Thermalito Union Elementary       Butte  KK-08     1550
  4:    61457 Golden Feather Union Elementary       Butte  KK-08      243
  5:    61523        Palermo Union Elementary       Butte  KK-08     1335
 ---                                                                     
416:    68957          Las Lomitas Elementary   San Mateo  KK-08      984
417:    69518            Los Altos Elementary Santa Clara  KK-08     3724
418:    72611          Somis Union Elementary     Ventura  KK-08      441
419:    72744               Plumas Elementary        Yuba  KK-08      101
420:    72751            Wheatland Elementary        Yuba  KK-08     1778
     teachers calworks   lunch computer expenditure    income   english  read
        <num>    <num>   <num>    <num>       <num>     <num>     <num> <num>
  1:    10.90   0.5102  2.0408       67    6384.911 22.690001  0.000000 691.6
  2:    11.15  15.4167 47.9167      101    5099.381  9.824000  4.583333 660.5
  3:    82.90  55.0323 76.3226      169    5501.955  8.978000 30.000002 636.3
  4:    14.00  36.4754 77.0492       85    7101.831  8.978000  0.000000 651.9
  5:    71.50  33.1086 78.4270      171    5235.988  9.080333 13.857677 641.8
 ---                                                                         
416:    59.73   0.1016  3.5569      195    7290.339 28.716999  5.995935 700.9
417:   208.48   1.0741  1.5038      721    5741.463 41.734108  4.726101 704.0
418:    20.15   3.5635 37.1938       45    4402.832 23.733000 24.263039 648.3
419:     5.00  11.8812 59.4059       14    4776.336  9.952000  2.970297 667.9
420:    93.40   6.9235 47.5712      313    5993.393 12.502000  5.005624 660.5
      math
     <num>
  1: 690.0
  2: 661.9
  3: 650.9
  4: 643.5
  5: 639.9
 ---      
416: 707.7
417: 709.5
418: 641.7
419: 676.5
420: 651.0

The cas dataset contains information on 420 public school districts in California, specifically those that operate either kindergarten through 6th grade (K–6) or kindergarten through 8th grade (K–8) schools, with data collected for the years 1998 and 1999.

The dataset includes:

Student performance measures (average reading and math scores).
School characteristics (such as enrollment, number of teachers, student–teacher ratio, number of computers, expenditure per student).
Student demographics (including income, percentage qualifying for reduced-price lunch, percentage of English learners, etc.).

cas is a data frame containing 420 observations on 14 variables. Refer to the following table for the full definition.

Variable	Description
`district`	Character. District code. Unique ID.
`school`	Character. School name.
`county`	Factor indicating county.
`grades`	Factor indicating grade span covered by the district’s schools. It takes on two values: - `KK-06`: means the district’s schools serve kindergarten through 6th grade. - `KK-08`: means the district’s schools serve kindergarten through 6th grade.
`students`	Total enrollment.
`teachers`	Number of teachers.
`calworks`	Percent qualifying for CalWorks (income assistance program).
`lunch`	Percent qualifying for reduced-price lunch.
`computer`	Number of computers.
`expenditure`	Expenditure per student.
`income`	District average income (in USD 1,000).
`english`	Percent of English learners (i.e., students for whom English is a second language).
`read`	Average reading score.
`math`	Average math score.

Data source: Stock, J. H. and Watson, M. W. (2020). Introduction to Econometrics, 4th ed. Pearson.

1.2 Summary Statistics

The following displays the summary for each variable in the dataset:

summary(cas)

    district        school                  county      grades   
 Min.   :61382   Length:420         Sonoma     : 29   KK-08:359  
 1st Qu.:64308   Class :character   Kern       : 27   KK-06: 61  
 Median :67760   Mode  :character   Los Angeles: 27              
 Mean   :67473                      Tulare     : 24              
 3rd Qu.:70419                      San Diego  : 21              
 Max.   :75440                      Santa Clara: 20              
                                    (Other)    :272              
    students          teachers          calworks          lunch       
 Min.   :   81.0   Min.   :   4.85   Min.   : 0.000   Min.   :  0.00  
 1st Qu.:  379.0   1st Qu.:  19.66   1st Qu.: 4.395   1st Qu.: 23.28  
 Median :  950.5   Median :  48.56   Median :10.520   Median : 41.75  
 Mean   : 2628.8   Mean   : 129.07   Mean   :13.246   Mean   : 44.71  
 3rd Qu.: 3008.0   3rd Qu.: 146.35   3rd Qu.:18.981   3rd Qu.: 66.86  
 Max.   :27176.0   Max.   :1429.00   Max.   :78.994   Max.   :100.00  
                                                                      
    computer       expenditure       income          english      
 Min.   :   0.0   Min.   :3926   Min.   : 5.335   Min.   : 0.000  
 1st Qu.:  46.0   1st Qu.:4906   1st Qu.:10.639   1st Qu.: 1.941  
 Median : 117.5   Median :5215   Median :13.728   Median : 8.778  
 Mean   : 303.4   Mean   :5312   Mean   :15.317   Mean   :15.768  
 3rd Qu.: 375.2   3rd Qu.:5601   3rd Qu.:17.629   3rd Qu.:22.970  
 Max.   :3324.0   Max.   :7712   Max.   :55.328   Max.   :85.540  
                                                                  
      read            math      
 Min.   :604.5   Min.   :605.4  
 1st Qu.:640.4   1st Qu.:639.4  
 Median :655.8   Median :652.4  
 Mean   :655.0   Mean   :653.3  
 3rd Qu.:668.7   3rd Qu.:665.8  
 Max.   :704.0   Max.   :709.5

Interpreting the Summary Statistics

This summary provides key insights into our dataset:

Continuous variables (students, teachers, expenditure, income, etc.) show their distribution through quartiles, mean, and range
Categorical variables (county, grades) show frequency counts
Notice the range of expenditure per student: from around \$3,900 to over \$7,700 - this substantial variation will be a key focus of our analysis
Test scores (reading and math) also show considerable variation, suggesting potential relationships with school resources

1.3 Expenditure Variation Analysis

Q: To what extent does expenditure per student vary?

Understanding the distribution of expenditure per student is crucial for education policy analysis. Let’s examine detailed descriptive statistics:

quick_summary <- function(x, full=FALSE) {
    # Function to compute basic descriptive statistics
    if (!full){
        # Basic summary
        data.frame(
          n = length(x),
          min = min(x),
          mean = mean(x),
          median = median(x),
          max = max(x),
          sd = sd(x),
          skewness = moments::skewness(x),
          kurtosis = moments::kurtosis(x),
          row.names = NULL
        )
    } else {
        # Full summary with quartiles and IQR
        data.frame(
          n = length(x),
          min = min(x),
          Q1 = quantile(x, 0.25),
          mean = mean(x),
          median = median(x),
          Q3 = quantile(x, 0.75),
          max = max(x),
          IQR = IQR(x),
          sd = sd(x),
          skewness = moments::skewness(x),
          kurtosis = moments::kurtosis(x),
          row.names = NULL
        )
    }
}
quick_summary(cas$expenditure) %>% round(2)

    n     min    mean  median     max     sd skewness kurtosis
1 420 3926.07 5312.41 5214.52 7711.51 633.94     1.07     4.88

Interpreting the Results:

Range: Expenditure varies from about \$3,926 to \$7,712 per student - a difference of nearly \$4,000
Central Tendency: The mean (\$5,312) is slightly higher than the median (\$5,196), suggesting a slight right skew
Variability: Standard deviation of \$633 indicates moderate spread around the mean
Skewness (1.07): Positive skewness confirms some districts spend considerably more than average
Kurtosis (4.88): Larger than 3 indicates a distribution with fat tails relative to the normal distribution.

# Basic histogram
ggplot(cas, aes(x = expenditure)) +
  geom_histogram(binwidth = 500, boundary = 0, fill = "lightblue", color = "black") +
  labs(title = "Histogram of Expenditure per Student",
       x = "Expenditure per Student (USD)",
       y = "Frequency") +
  theme_minimal(base_size = 14)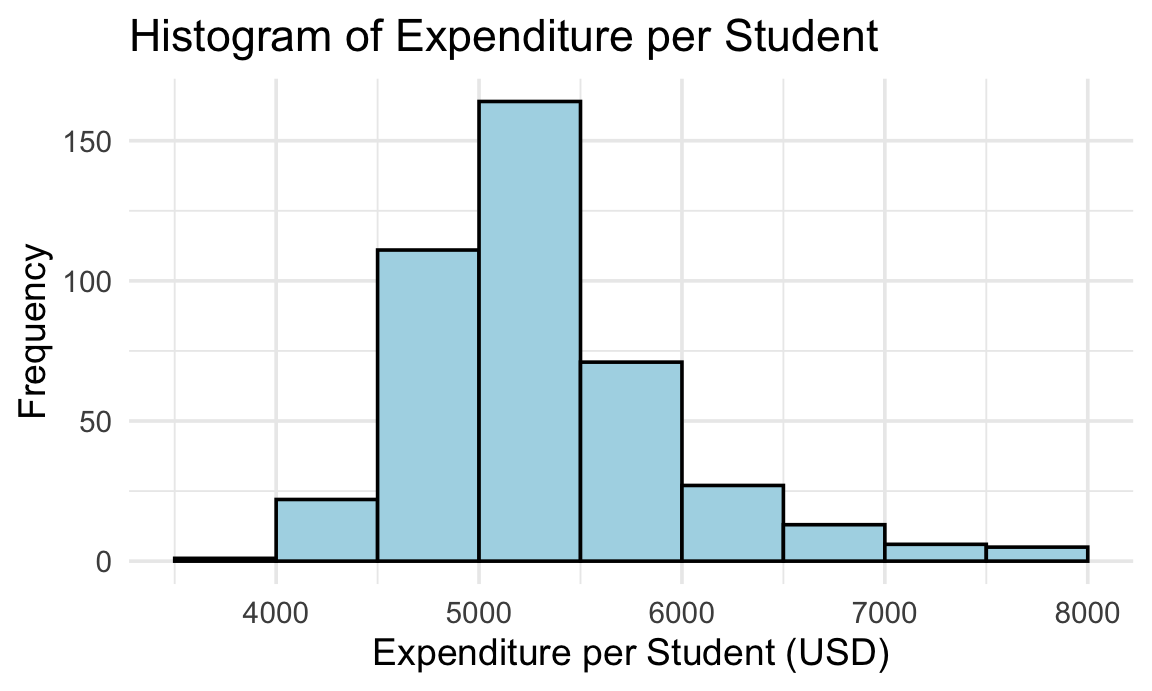

What the Histogram Reveals:

Most districts cluster around the \$5,000-\$5,500 range
Variability is moderate
The distribution has a long right tail, indicating positive skewness. That suggests that expenditure per student is concentrated at lower values for most districts, while a smaller number of districts spend substantially more, pulling the mean above the median
There are few extreme positive outliers, indicating some districts do spend significantly more than average

1.4 Group Comparison: K-6 vs K-8 Schools

Q: Are there any differences in expenditure per student between K-6 and K-8 schools?

This comparison helps us understand whether grade span affects resource allocation. Let’s examine the statistics for each group:

cas %>%
    group_by(grades) %>%
    group_map(~ {
        s <- quick_summary(.x$expenditure, full=TRUE)
        s <- cbind(
            grades = .y$grades,    # add group info
            s)
        return(s)
    }) %>%
    bind_rows()

  grades   n      min       Q1     mean   median       Q3      max      IQR
1  KK-08 359 3926.070 4881.139 5267.365 5195.919 5539.380 7711.507 658.2412
2  KK-06  61 4715.446 5092.917 5577.493 5399.383 5990.794 7614.379 897.8770
        sd skewness kurtosis
1 618.6415 1.094514 5.284716
2 662.8033 1.019435 3.309185

Key Findings:

K–6 schools (61 districts): Mean expenditure of \$5,577, slightly higher than K–8 schools
K–8 schools (359 districts): Mean expenditure of \$5,267, with a larger sample size
K–6 schools indicating higher variability, with a standard deviation of \$662 compared to \$618 for K-8 schools
Skewness is positive for both groups, with K–8 schools showing slightly more skewness
The difference suggests that smaller grade span districts may have slightly higher per-pupil spending

Box plot by grades span

ggplot(cas, aes(x = grades, y = expenditure, fill = grades)) +
  geom_boxplot() +
  scale_fill_npg() +
  labs(x = "Grade Span",
       y = "Expenditure per Student (USD)") +
  theme_minimal(base_size = 14) +
  theme(legend.position = "none")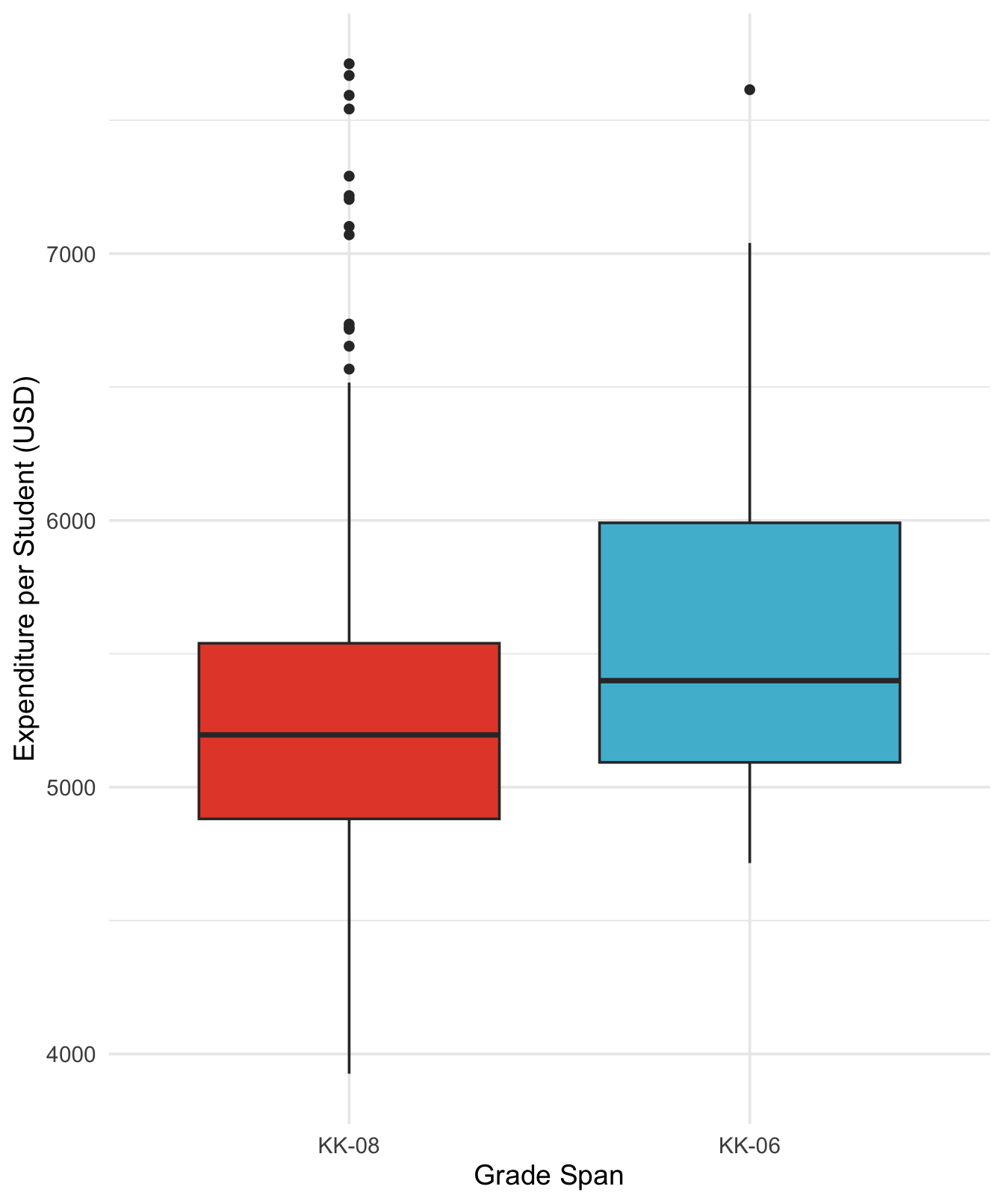

Understanding the Box Plot:

1. Box and middle bar (median)

The box itself spans from the first quartile (Q1, 25th percentile) to the third quartile (Q3, 75th percentile).
This range is called the interquartile range (IQR = Q3 - Q1).
The middle bar inside the box represents the median (50th percentile).
- If the median is closer to the bottom of the box, the lower half of the data is more concentrated.
- If closer to the top, the upper half is more concentrated.

2. Whiskers

The whiskers extend from the box to show the range of the data excluding outliers.
A whisker extends to the largest/smallest value within 1.5 × IQR from the box:
- Upper whisker = largest value ≤ Q3 + 1.5 × IQR
- Lower whisker = smallest value ≥ Q1 - 1.5 × IQR

3. Outliers

Points beyond the whiskers are plotted individually as outliers.
These are values that are unusually high or low relative to the bulk of the data.

Summary of boxplot

Box: middle 50% of the data
Middle line: median
Whiskers: typical range, excluding extreme values
Outliers: extreme observations

Interpreting the Box Plot:

Median lines: K–6 districts show a higher median expenditure than K-8 districts
Box sizes: K–6 district show a larger interquartile ranges (IQR), indicating greater middle 50% spread
Outliers: K–8 groups show more positive outliers (points beyond the whiskers), representing districts with unusually high expenditure

1.5 Correlation Analysis

Q: What predicts expenditure per student?

Understanding which factors correlate with expenditure helps identify patterns in educational resource allocation. Let’s examine correlations:

Correlation coefficients in ascending order:

# Get the set of numeric variables
v <- setdiff(
    names(cas),
    c("district", "school", "county", "grades")
)
corExp <- cor(cas["expenditure"], cas[setdiff(v, "expenditure")])
t(corExp) %>%
    as.data.frame() %>%
    rownames_to_column(var = "variable") %>%
    rename(correlation = expenditure) %>% 
    arrange(correlation)

  variable correlation
1 students -0.11228455
2 teachers -0.09519483
3  english -0.07139604
4 computer -0.07131050
5    lunch -0.06103871
6 calworks  0.06788857
7     math  0.15498949
8     read  0.21792682
9   income  0.31448448

Key Correlation Insights:

No strong correlations (e.g., $>|0.7|$) with expenditure
Positive correlations: Income (0.31), math scores (0.22), and reading scores (0.15)
Moderate Negative correlations: Students($-0.11$), indicating districts with a larger amount of students tend to spend less per student
Interpretation:
- Wealthier districts tend to spend more per student
- Higher spending correlates with better test scores
- Districts with more students may face budget constraints leading to lower per-student expenditure

Plot scatter plots for the top three correlated variables

top_vars <- c("income", "math", "read")
cas_long <- cas %>%
    select(expenditure, all_of(top_vars)) %>%
    pivot_longer(cols = all_of(top_vars), names_to = "variable", values_to = "value")
ggplot(cas_long, aes(x = value, y = expenditure)) +
    geom_point(alpha = 0.6, color = "#1976d2") +
    facet_wrap(~variable, scales = "free_x") +
    labs(
        title = "Scatter Plots of Expenditure per Student vs. Top Correlated Variables",
        x = "Value",
        y = "Expenditure per Student (USD)"
    ) +
    theme_minimal(base_size = 14)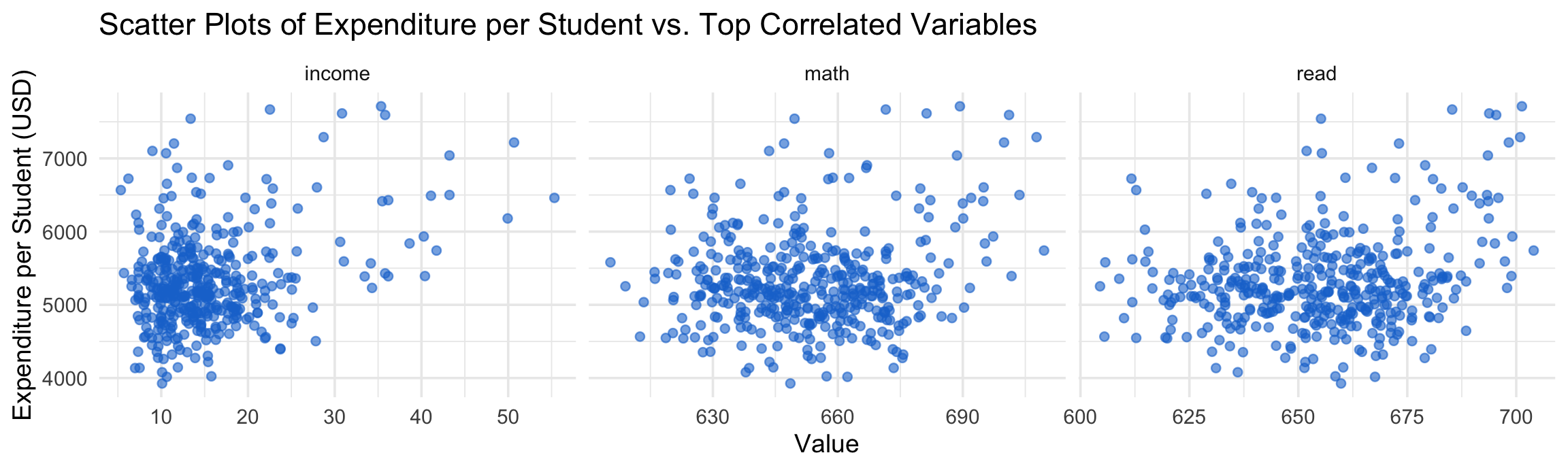

What These Scatter Plots Reveal:

Income vs. Expenditure: Positive relationship - wealthier districts consistently spend more per student; the trend is relatively clear with some variability;
Math Scores vs. Expenditure: Positive trend suggests higher spending correlates with better math performance; the points are more scattered, indicating other factors also play a role;
Reading Scores vs. Expenditure: Similar pattern to math scores, showing the relationship between resources and achievement
Data Distribution: Points are fairly scattered, indicating that while correlations exist, other factors also influence these relationships

1.6 Academic Performance Relationship

Q: what is the relationship between district level maths and reading scores?

Academic performance across different subjects often correlates, as they reflect overall educational quality and student preparation. Let’s examine this relationship:

with(cas, cor.test(math, read))


    Pearson's product-moment correlation

data:  math and read
t = 49.005, df = 418, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.9073417 0.9359362
sample estimates:
      cor 
0.9229015

ggplot(cas, aes(x = read, y = math)) +
    geom_point(alpha = 0.6, color = "#1976d2") +
    geom_smooth(method = "lm", color = "#d32f2f") +
    labs(
        title = "Scatter Plot of Math vs. Reading Scores",
        x = "Average Reading Score",
        y = "Average Math Score"
    ) +
    theme_minimal(base_size = 14)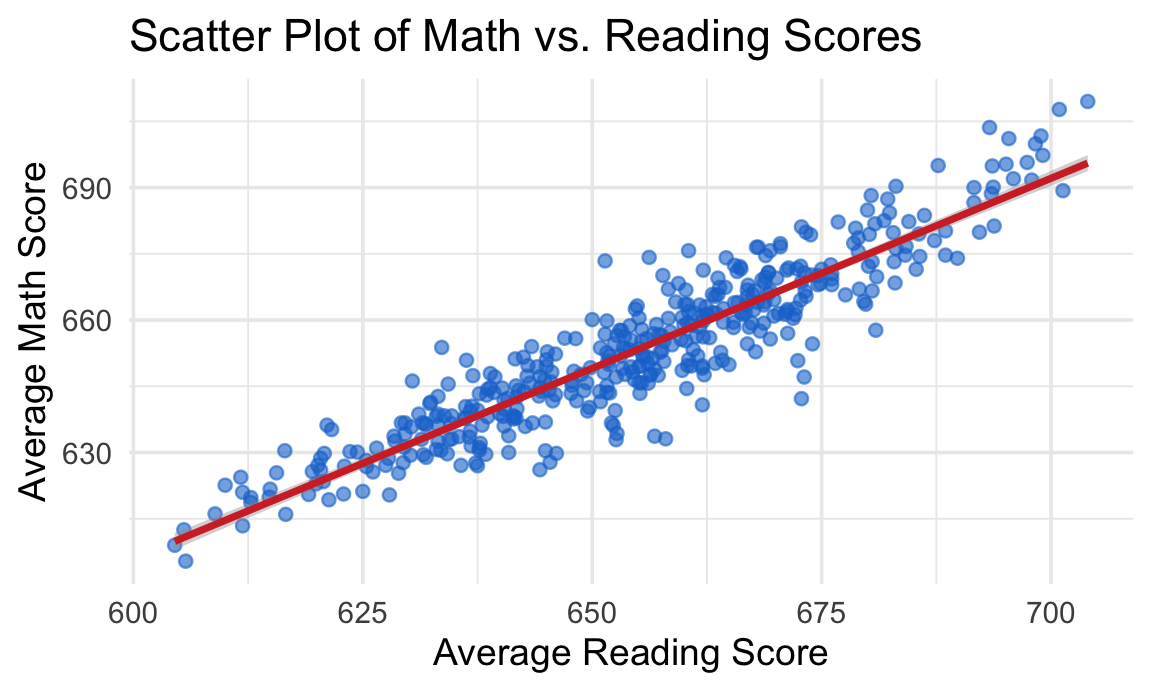

Analysis of the Relationship:

Strong positive correlation: Districts with higher reading scores typically have higher math scores
Linear trend: The smooth line shows a clear linear relationship between the two subjects
Tight clustering: Most points cluster closely around the trend line, indicating a strong relationship
Educational insights:
- This suggests that factors affecting academic performance impact multiple subjects similarly
- Districts that excel in one area tend to excel in others

2 Q-Q Plot

The Q-Q plot, or quantile-quantile plot, is a graphical tool to help us assess if a set of data plausibly came from some theoretical distribution such as a normal distribution.

Understanding Q-Q Plots:

A QQ plot is a scatter plot created by plotting two sets of quantiles against one another.

If both sets of quantiles came from the same distribution, we should see the points forming a line that’s roughly straight.
For example, if we run a statistical analysis that assumes our residuals are normally distributed, we can use a normal QQ plot to check that assumption.

When the theoretical quantiles are from a normal distribution, the plot is called a normal QQ plot.

Why Q-Q Plots Matter:

Many statistical tests assume normality; deviations from normality can affect the validity of statistical inferences
Q-Q plots provide a visual method to assess these assumptions
They help identify the type of non-normality (skewness, heavy tails, etc.)

2.1 QQ plot visualization tool

https://xiongge.shinyapps.io/QQplots/

Adjust Skewness and Kurtosis to see how the QQ plot changes.
Note the website is not able to host many users at the same time, so if it does not load, please try again later.

2.2 Skewness

Positive skew

Positively skewed (mean > median) data have a J-shaped pattern in the Q-Q plot.

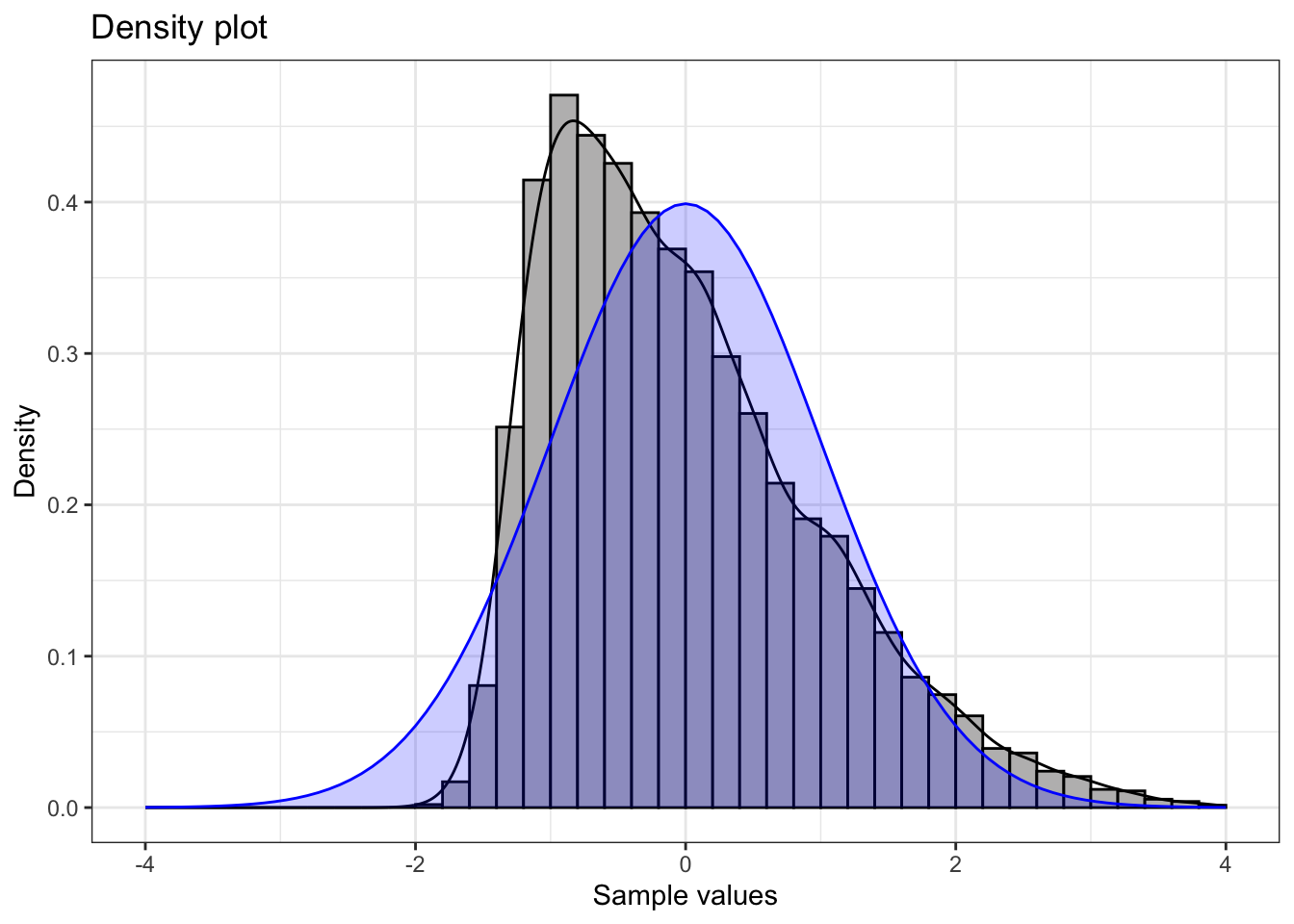
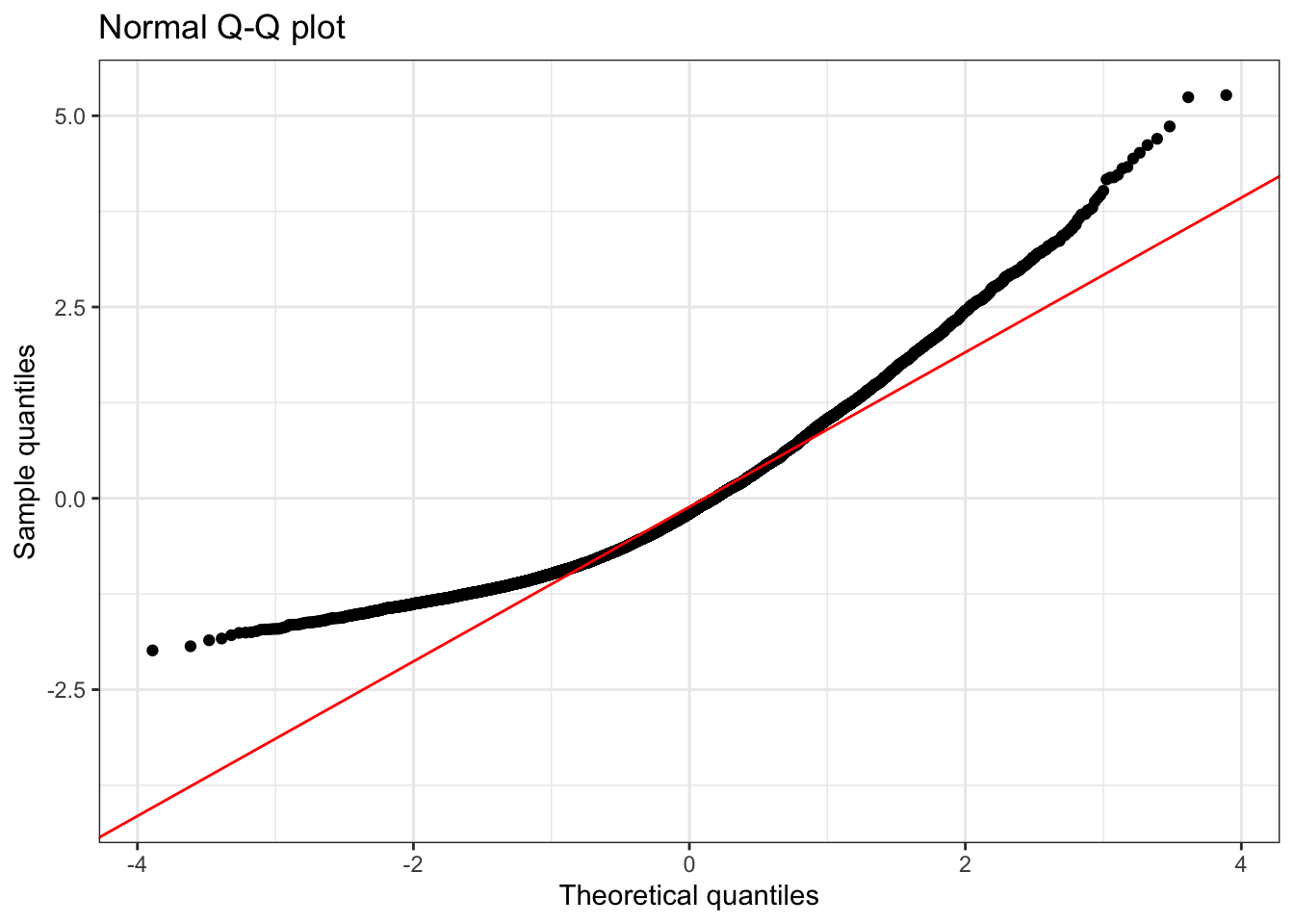
Summary statistics:

      n   min  mean median  max   sd skewness kurtosis
1 10000 -1.99 -0.01   -0.2 5.27 1.01     0.93     3.79

💡 Note that for a positive skewed distribution, the mean is larger than the median because the long right tail pulls the mean above the median.

Understanding Positive Skewness:

Shape: Long tail extending to the right
Mean vs. Median: Mean > Median (tail pulls the mean upward)
Q-Q Plot Pattern: J-shaped curve, points above the line at both ends
Real-world examples: Income distribution, housing prices
Statistical implications: May indicate floor effects or bounded distributions

Negative skew

Negatively skewed (mean < median) data have Q-Q plots that display an inverted J-shape.

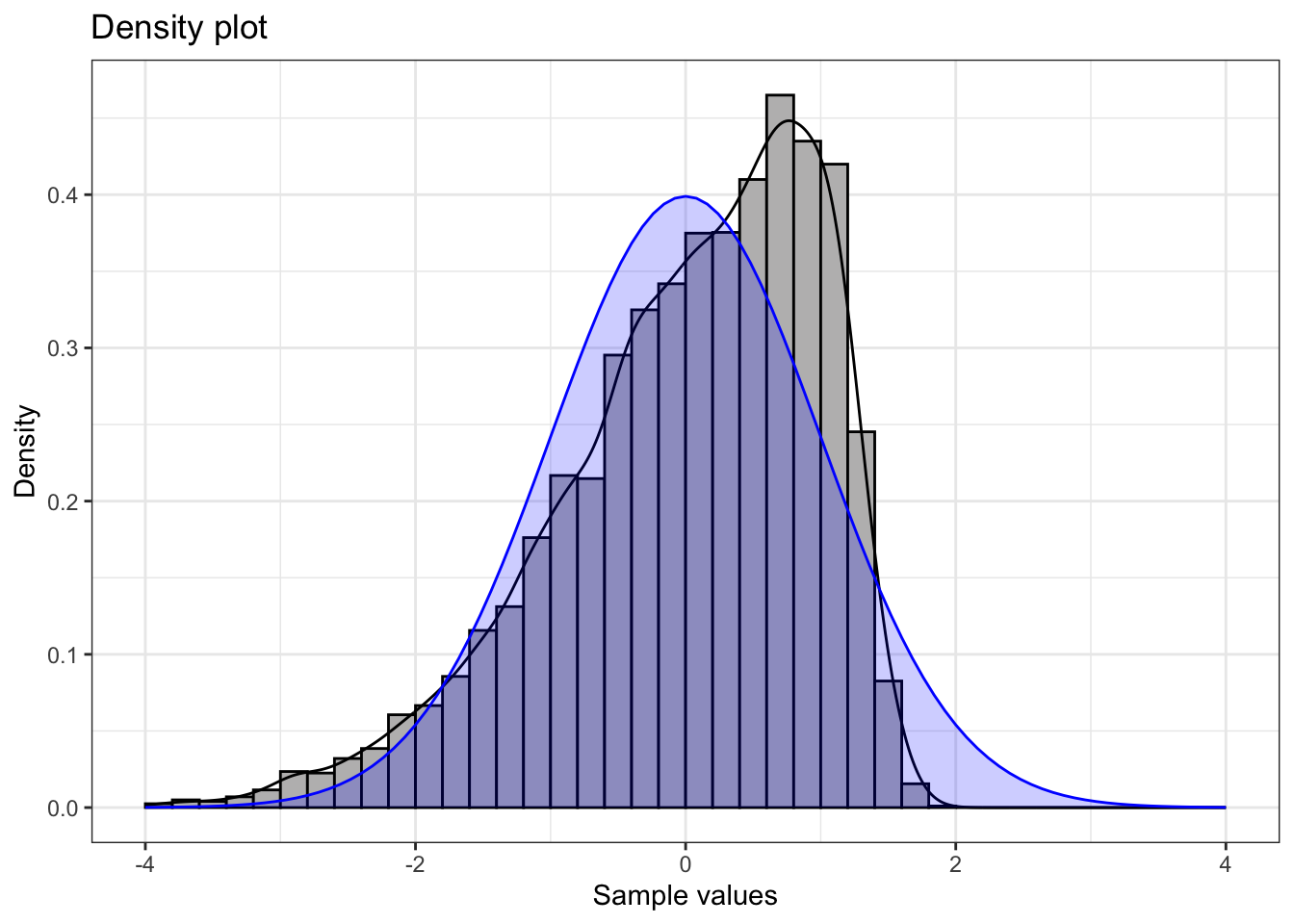
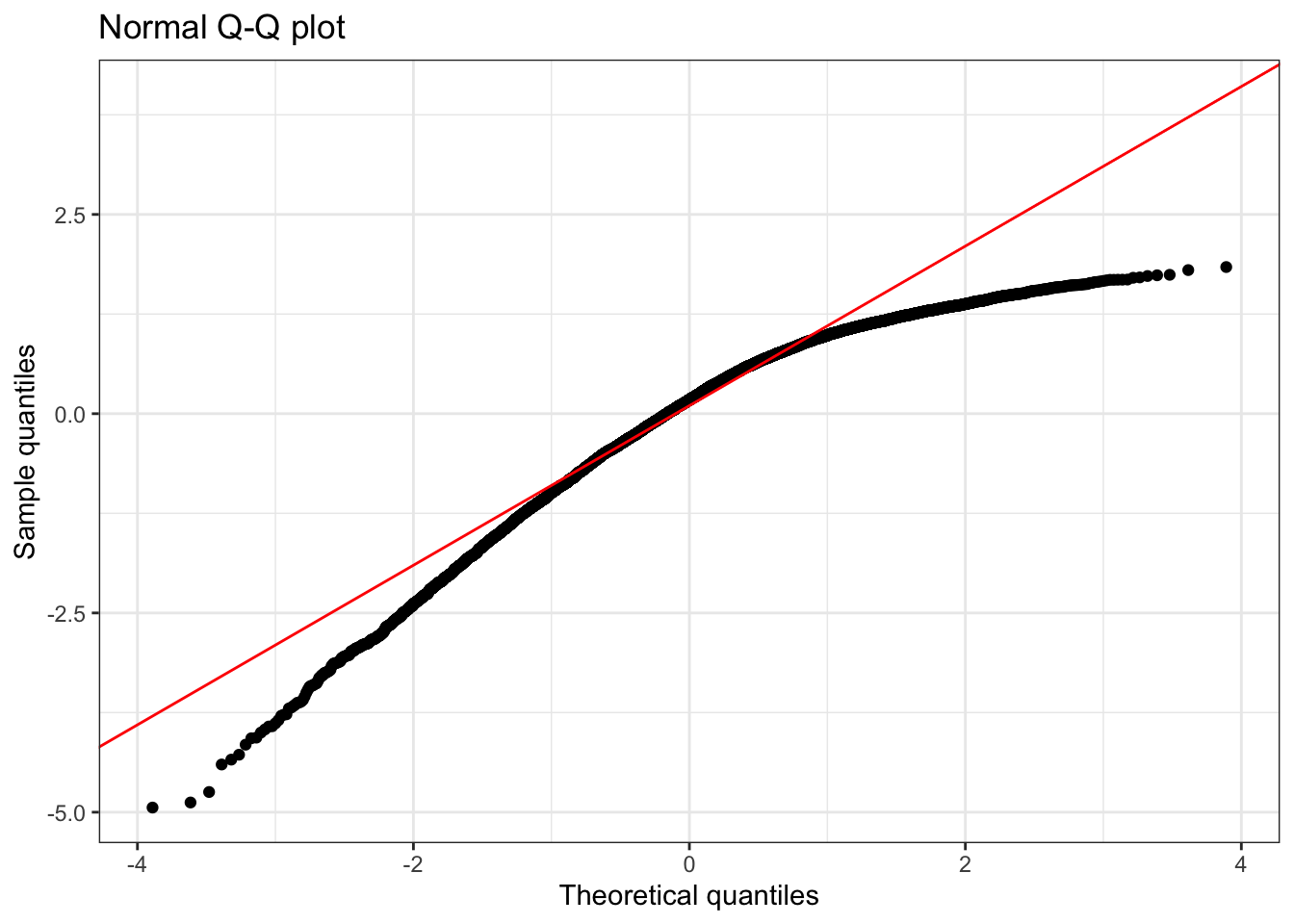
Summary statistics:

      n   min mean median  max   sd skewness kurtosis
1 10000 -4.94    0   0.17 1.84 0.99    -0.89     3.67

💡 Note that for a negatively skewed distribution, the mean is smaller than the median because the long left tail pulls the mean above the median.

Understanding Negative Skewness:

Shape: Long tail extending to the left
Mean vs. Median: Mean < Median (tail pulls the mean downward)
Q-Q Plot Pattern: Inverted J-shaped curve, points below the line at both ends
Real-world examples:
- Test scores (when most students perform well): Most students score high (80-100), with fewer low scores creating a left tail
- Age at retirement: Most people retire around 65-67, but some retire much earlier due to health or financial reasons
Statistical implications: May indicate ceiling effects or bounded distributions

2.3 Kurtosis

Kurtosis measures the “tailedness” of a distribution compared to a normal distribution. Understanding kurtosis helps identify distributions with unusually many or few extreme values.

Fat tails

This plot shows a t-distribution with $3$ degrees of freedom, which has heavier tails than a normal distribution.

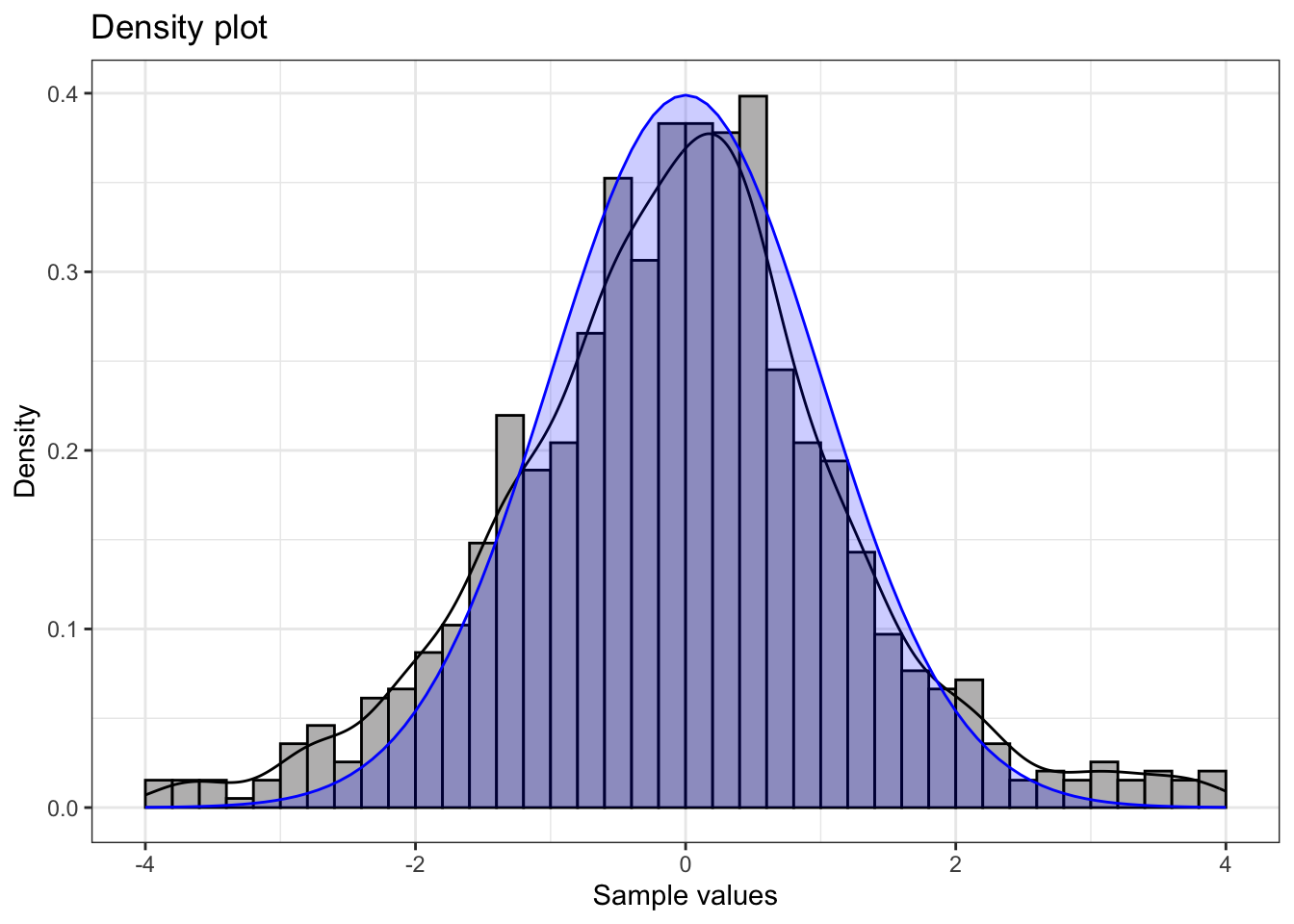
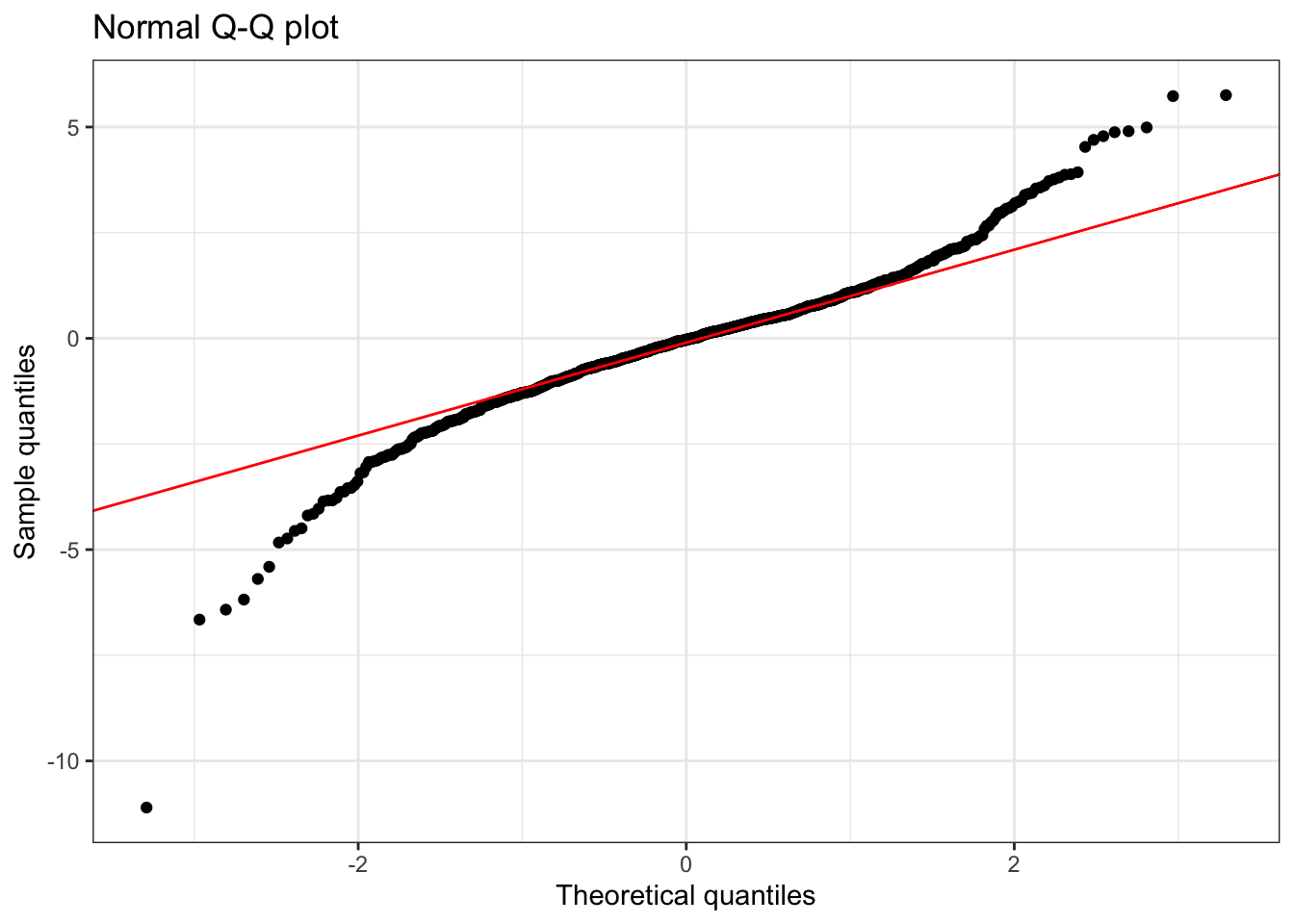
Summary statistics:

     n   min  mean median  max   sd skewness kurtosis
1 1000 -11.1 -0.09  -0.03 5.75 1.48    -0.51     8.15

Understanding Fat Tails (High Kurtosis):

Q-Q Plot Pattern: Reverse S-shaped curve - points below the line at low quantiles, above at high quantiles.
Kurtosis > 3: Indicates heavier tails than normal distribution
Practical meaning: More extreme values (both high and low) occur than expected under normality
Real-world examples:
- Financial returns: Stock market crashes and booms occur more frequently than normal distribution predicts
- Measurement errors: Occasionally very large errors occur due to equipment malfunction or human mistakes
- Response times: Most responses are quick, but some take much longer due to system overload or user distraction
Statistical implications: Higher risk of extreme events; standard confidence intervals may be too narrow

Thin tails

This example shows a distribution with lighter tails than normal.

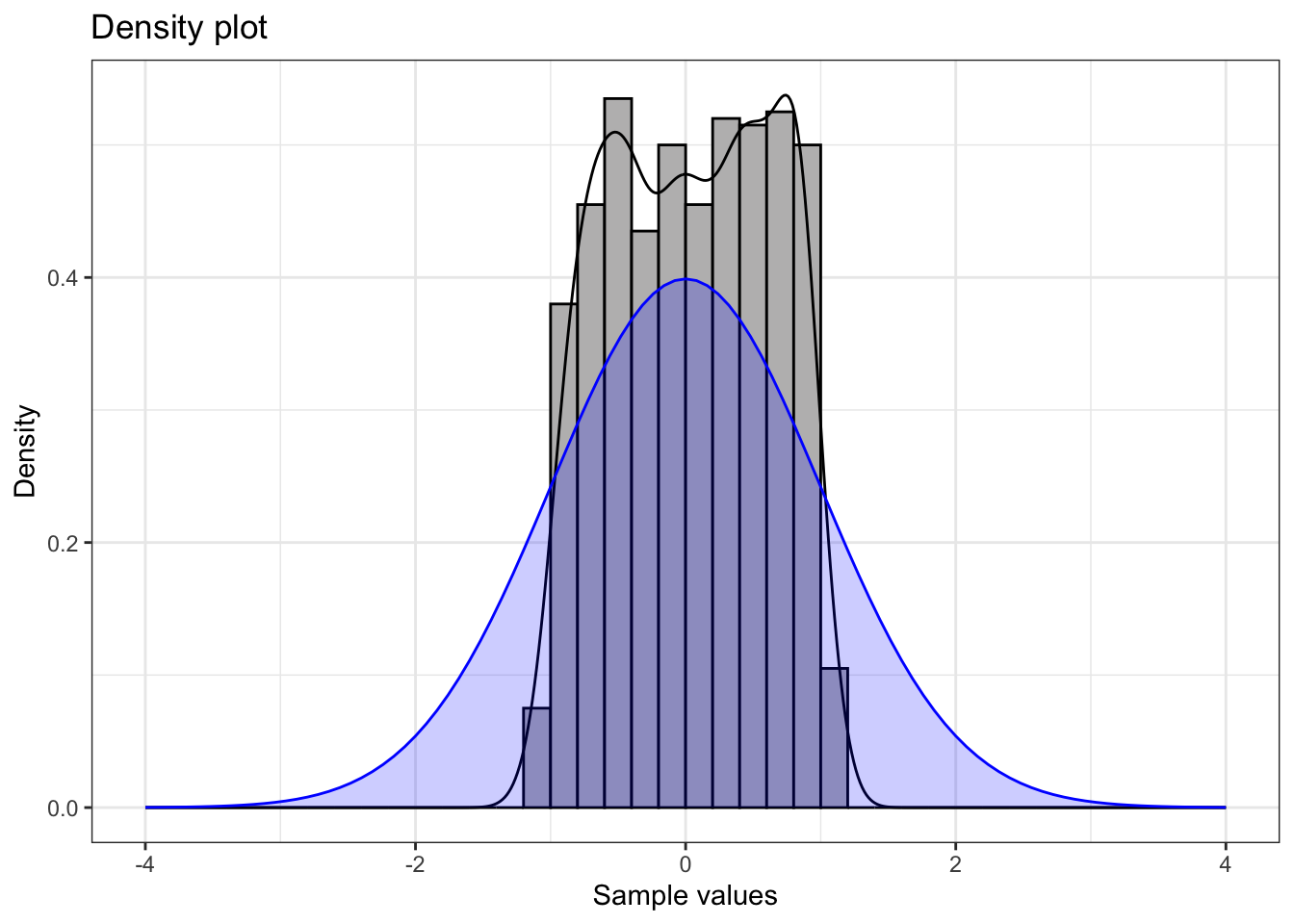
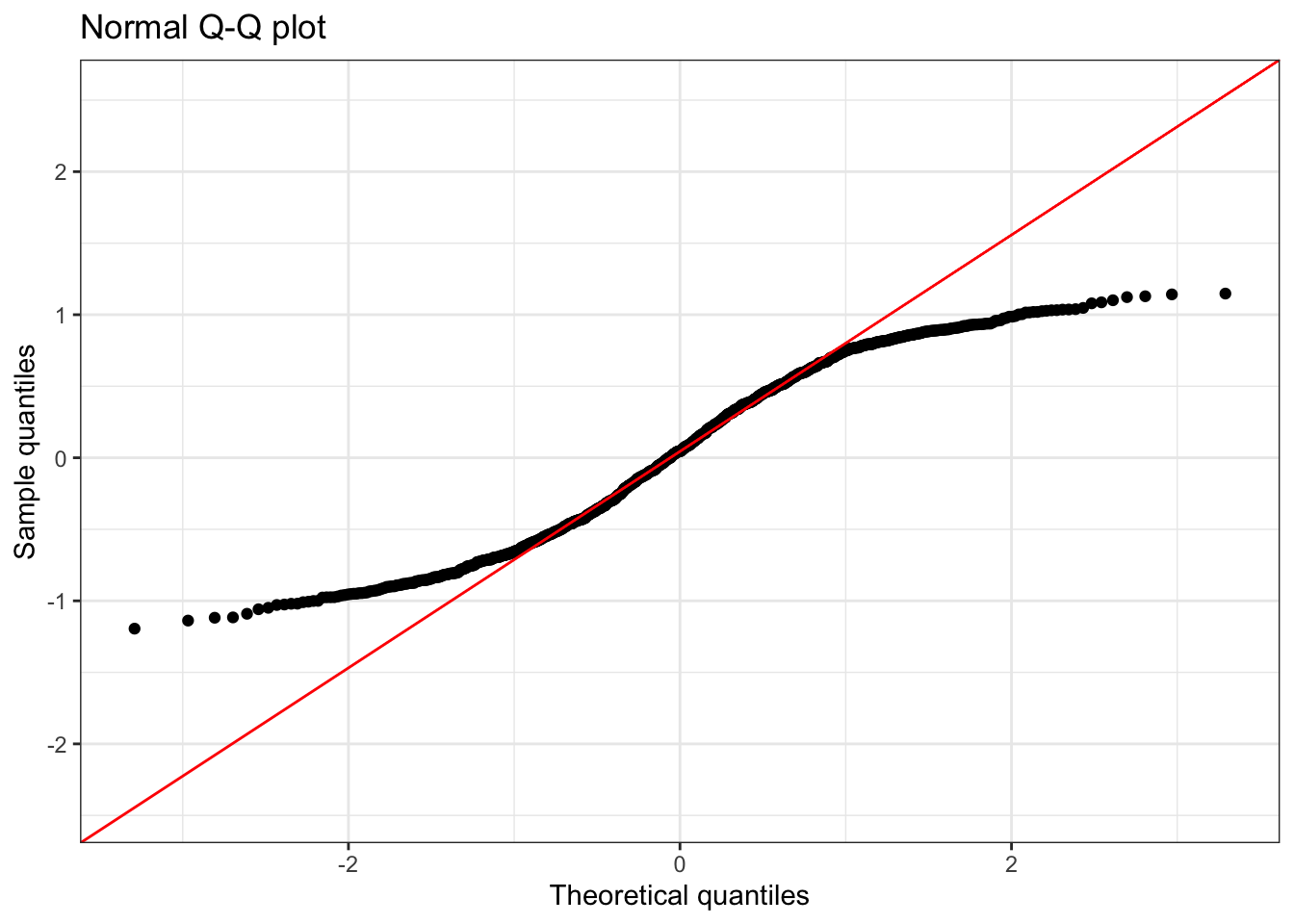
Summary statistics:

     n   min mean median  max   sd skewness kurtosis
1 1000 -1.19 0.04   0.05 1.15 0.59    -0.06      1.8

Understanding Thin Tails (Low Kurtosis):

Q-Q Plot Pattern: S-shaped curve - points above the line at low quantiles, below at high quantilees.
Kurtosis < 3: Indicates lighter tails than normal distribution
Practical meaning: Fewer extreme values occur than expected under normality
Real-world examples: Bounded measurements, standardized test scores, some quality control data
Statistical implications: Lower risk of extreme events; data more predictable than normal assumption suggests

Summary of Distribution Shapes

Understanding these patterns helps in:

Choosing appropriate statistical methods
Identifying data quality issues
Making informed assumptions about uncertainty
Selecting proper transformations when needed
Interpreting results correctly in context

1 Descriptive Analysis and Data Visualization with CASchools

1.1 Dataset Overview

1.2 Summary Statistics

1.3 Expenditure Variation Analysis

1.4 Group Comparison: K-6 vs K-8 Schools

Box plot by grades span

1.5 Correlation Analysis

1.6 Academic Performance Relationship

2 Q-Q Plot

2.1 QQ plot visualization tool

2.2 Skewness

Positive skew

Negative skew

2.3 Kurtosis

Fat tails

Thin tails

1 Descriptive Analysis and Data Visualization with `CASchools`